光线追踪中需要用到几何的知识点,在这简单描述下涉及到的一些知识点
Geometry
表现几何的多种方法:
Implicit(隐性)
隐形几何方程可以表示空间中的一些点之间的关系,但是没有实际的点可以告诉你,方程如下:
很容易可以判断某一个点是否在不在表面上: x = ? y = ? z = ?
若f(x,y,z) < 1 在物体内
若f(x,y,z) > 1 在物体外
若f(x,y,z) = 1 在物体表面上
\[f(x,y,z) = x^2+y^2+z^2 = 1\]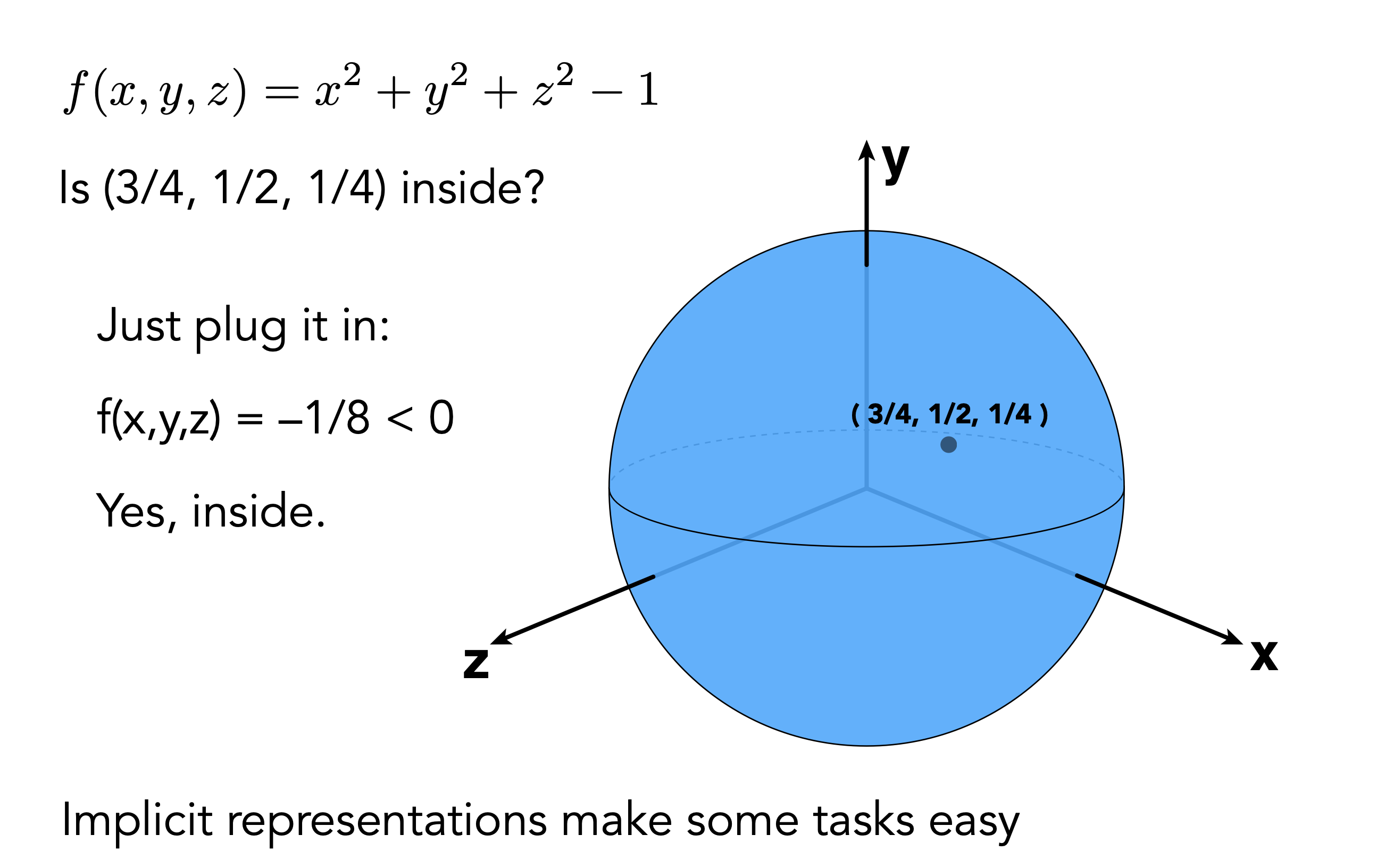
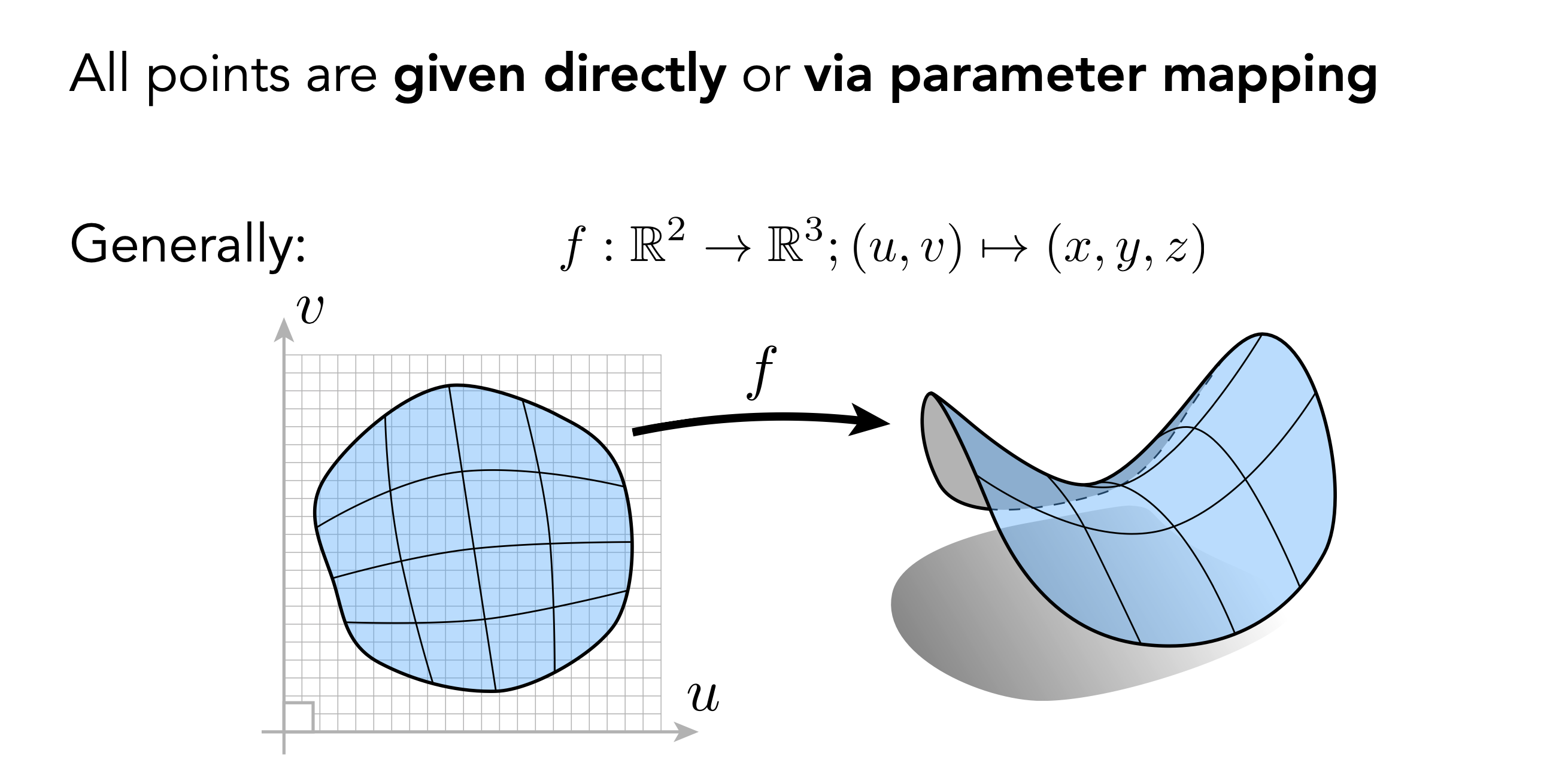
Explicit(显性)
定义一个函数,2D维度的贴图UV位置通过函数映射到3D维度坐标的面模型
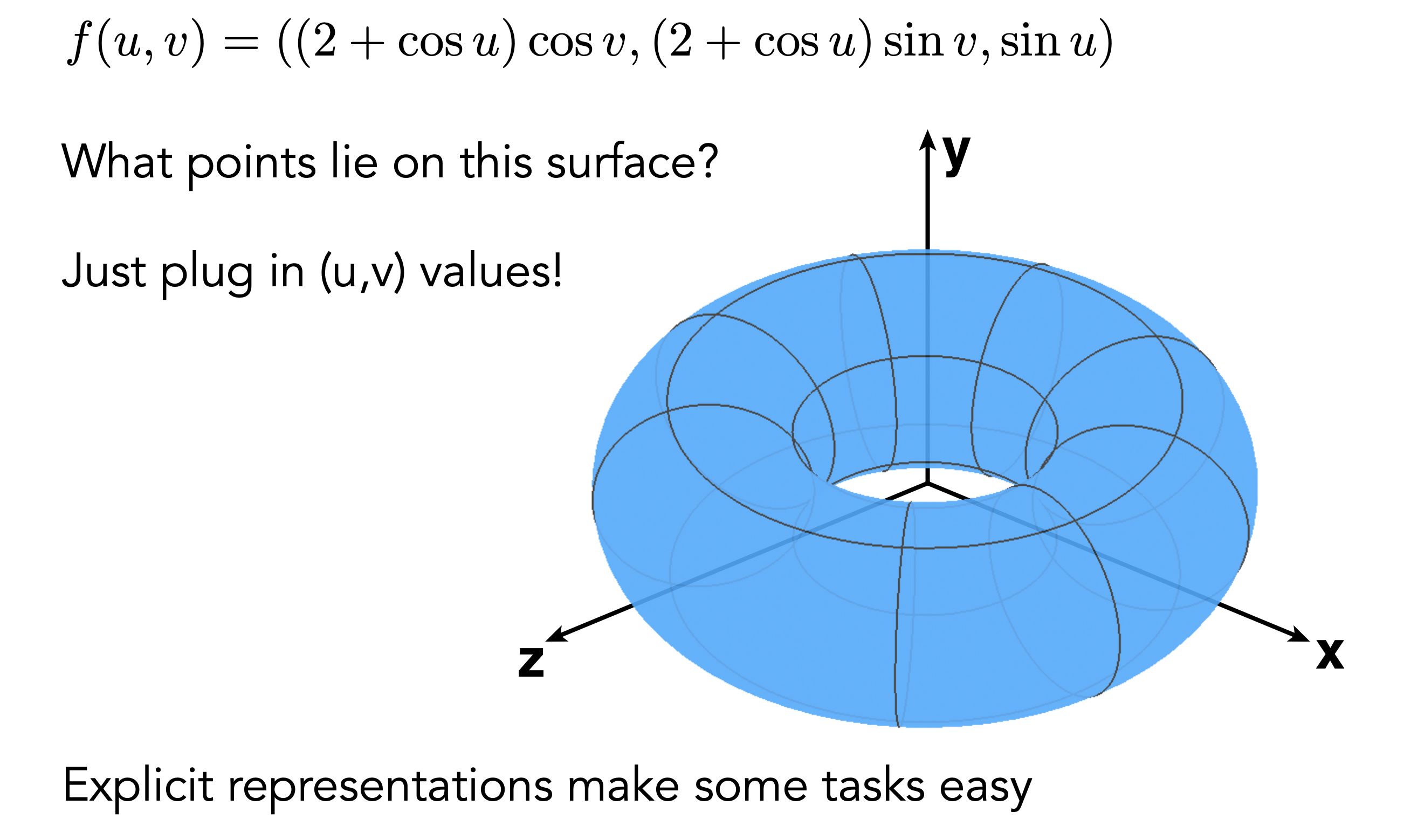
Ray Tracing
Whitted-Style Ray Tracing
光线追踪是指我们反向的虚拟一条从人眼出发的光线到我们看到的物体,在打到的物体上,再连接一条路径到光源,看这条路径是否能直接到达光源,没有被物体遮挡,如果到达光源,那么就表示这个物体能被光源照亮,然后我们再对这个物体进行着色。
以上过程就是光源发出光线打到一个物体再到我们眼睛的路径的反向过程.
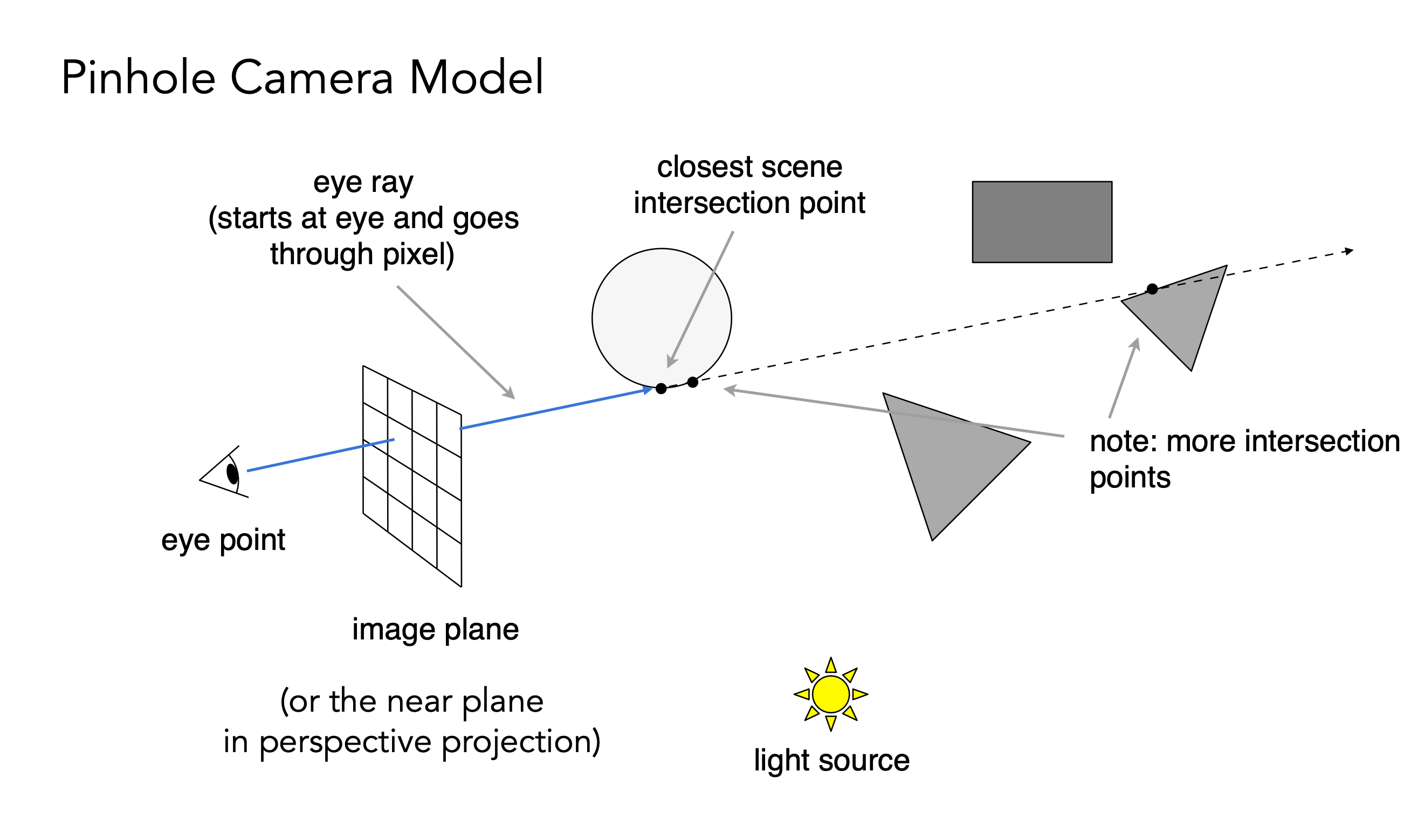
当然,光线也有可能是光源->物体->n个物体反射->物体->眼睛这么一个路径,所以我们看到的物体可能是很多条这样不同的路径的光线汇聚而成照亮再反射到我们眼睛,因此屏幕上的一个像素的着色可以是很多条光线路径汇聚而成.
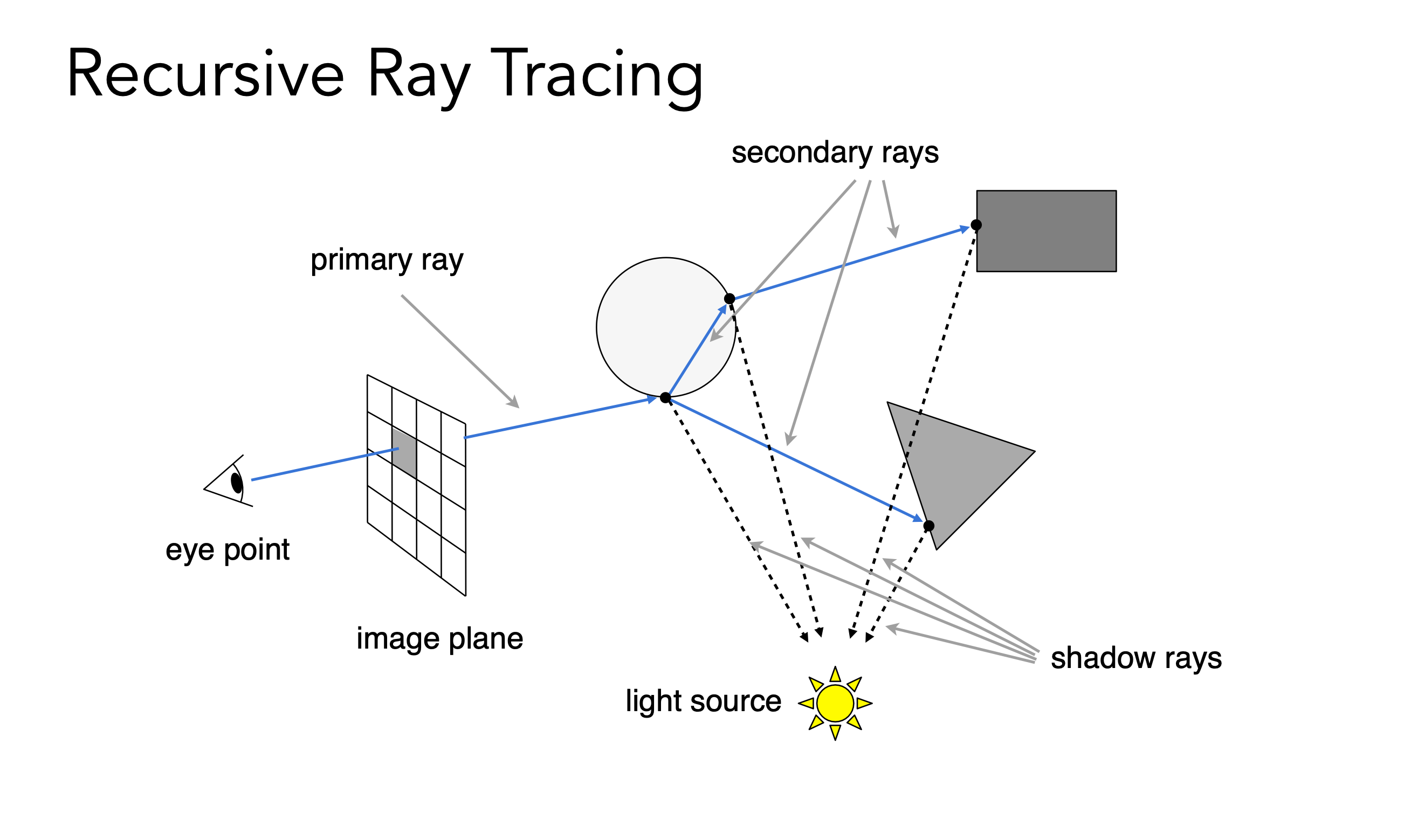
Ray-Surface Intersection
光-表面交点
那么,上面这个过程我们需要知道光的路径和物体表面相交是怎么计算的,就需要以下的方程:
 \(r(t) =o +td\) 从光源坐标出发,往某一个方向d经过时间t的距离,这就描述来一个光线发射的射线向量
\(r(t) =o +td\) 从光源坐标出发,往某一个方向d经过时间t的距离,这就描述来一个光线发射的射线向量
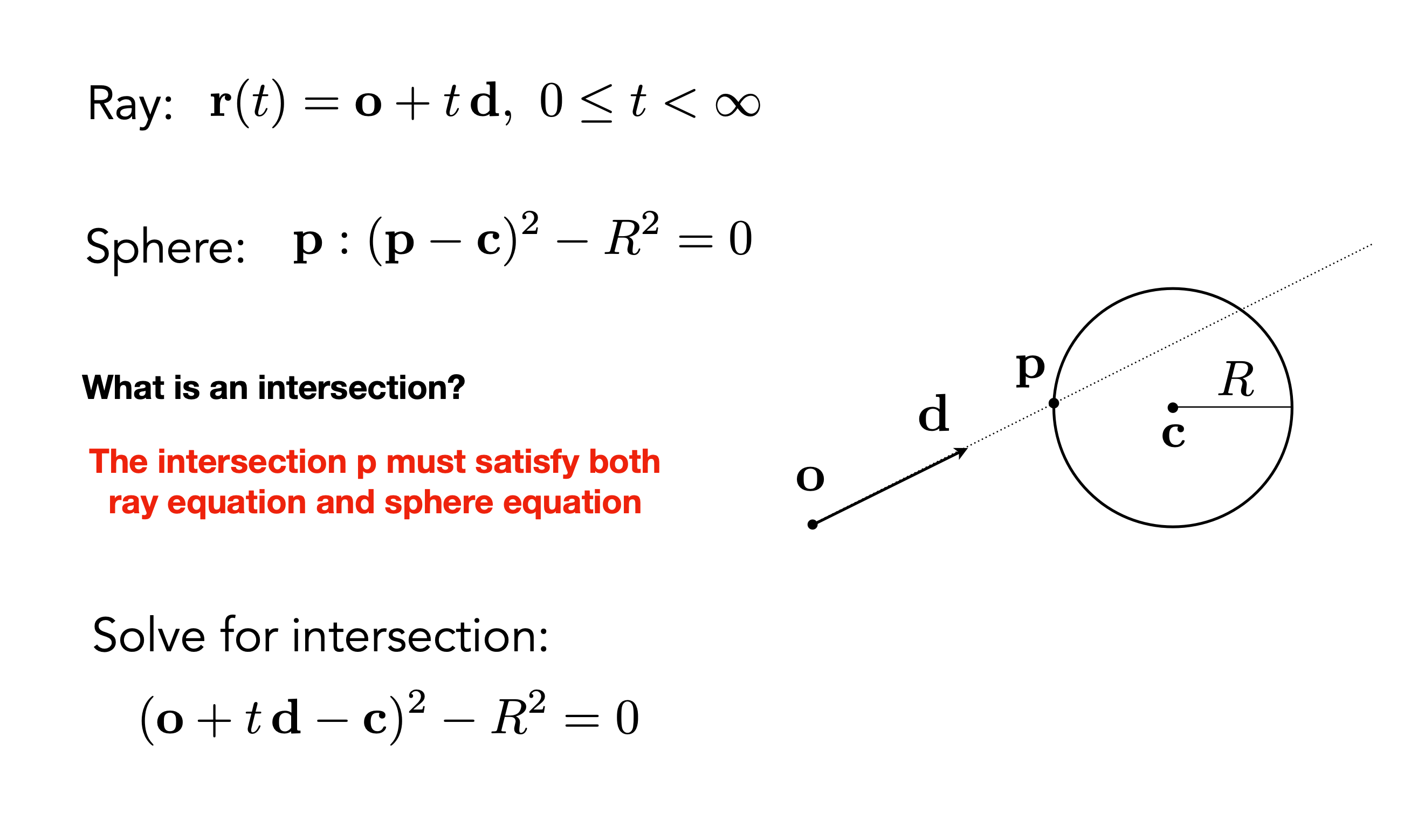
隐式表面
如果光线和一个物体相交,如果有交点p,那么用上面简述过的物体几何方程与光线方程做代入,隐式的几何方程可以求某一个点是否在表面上,就有以下式子: \((r(t)-c)^2-R^2=0\) 球的定义方程(球上的一个点p到球的中心c的距离平方等于半径R平方): \((p-c)^2-R^2 = 0\) 若射线与球表面有交点,则点P等于射线r(t): \(p = r(t)\) 
求出t,根据射线方程,就可以将P点球出来
另外将光线和不同的隐式表面方程求交,就可以解出不同形状的物体交点的值

显示表面
光线与三角形求交,当我们知道模型表面三角形的坐标值,求与物体三角形的交点,求出与三角形相交最小的t,就是最近的那个三角形,但是这种方法计算量非常大,模型表面有非常多的三角形,速度将会非常慢
射线与模型求交,如果交点数是偶数,那就是在模型外,如果交点数是奇数,那就是在模型内
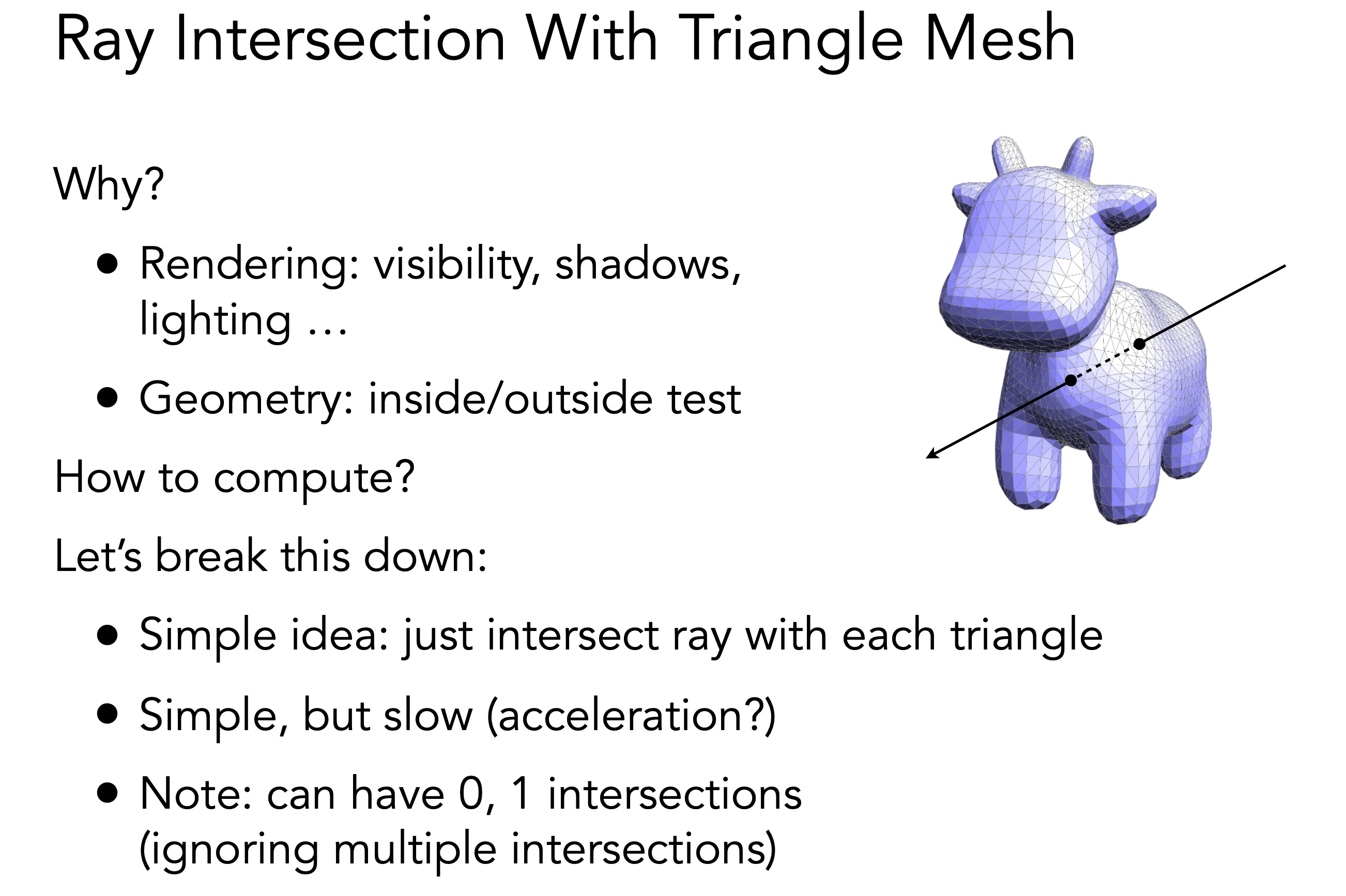
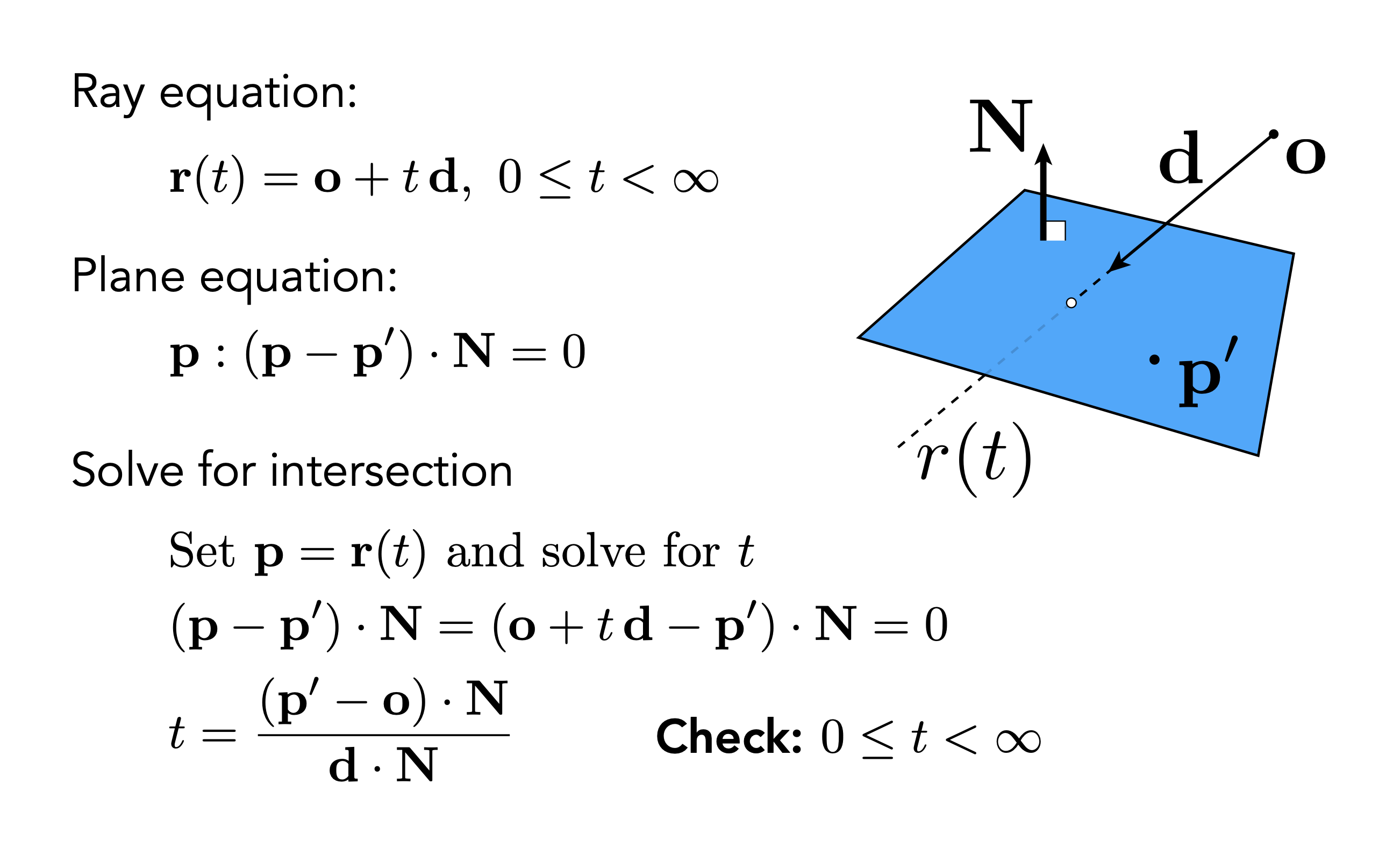
射线与三角形求交,三角形在一个平面内,我们可以和平面求交,再判断交点是否在三角形内
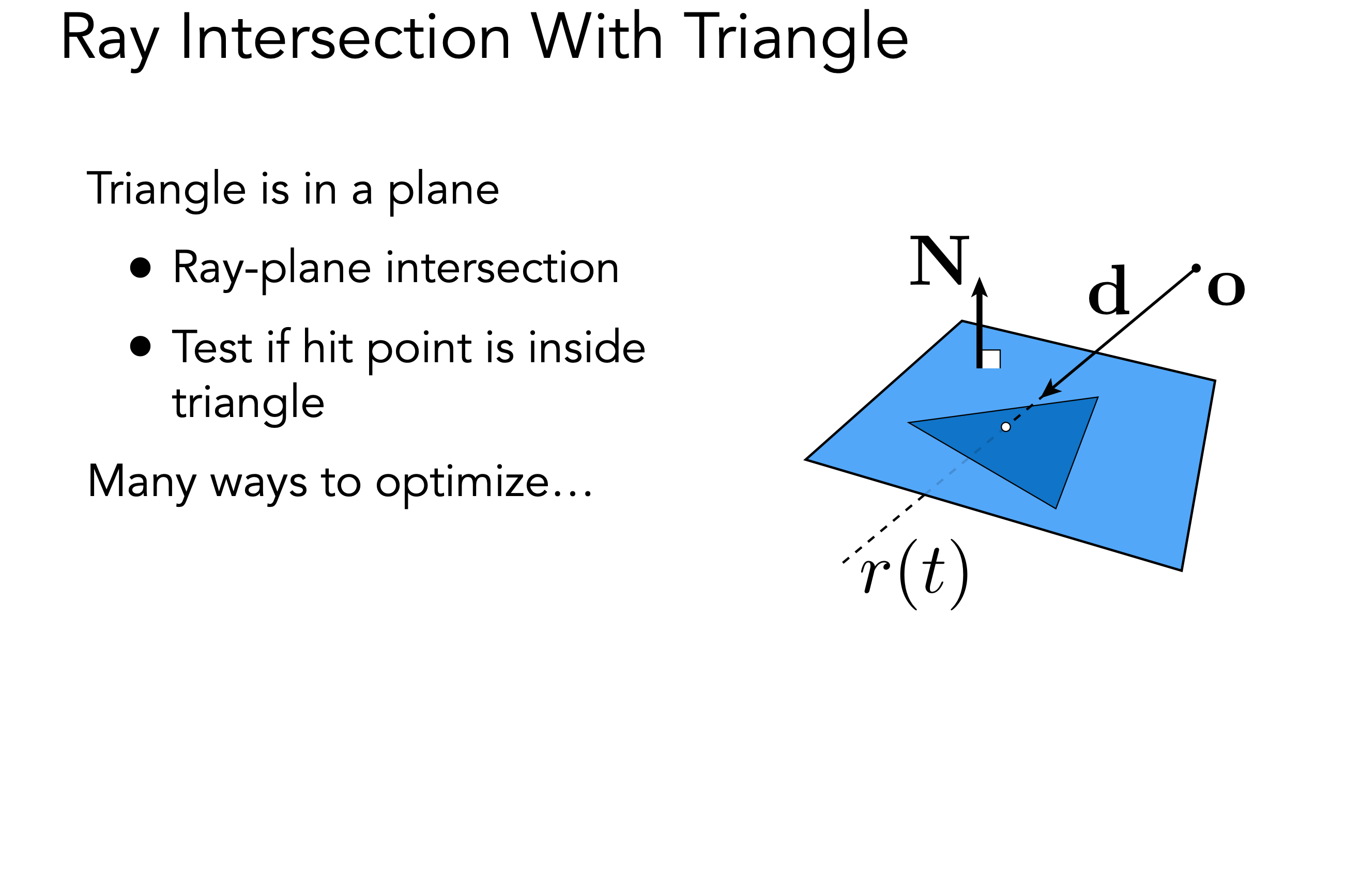
假设射线和平面有一个交点,我们知道平面法线和平面上的点,平面上任何一个点减去交点得到一个向量,若这个向量和法线垂直,表示这个向量在平面内,交点也在平面内
Möller Trumbore Algorithm
当然,还有更简单的方法
我们知道三角形的三个顶点,所以可以用重心坐标来描述三角形内的任何一个点,我们知道重心坐标是用alpaha、beta、gama与三个顶点坐标插值出内部任何一个点,alpha+beta+gama=1,那么就可以将将其描述为alpha,beta,gama = 1- alpha - gama,这样我们就只有两个未知参数,就可以获得如下的公式:

如果光线与三角形有交点,那么肯定满足以上公式,只要解出t、b1、b2就可以得到交点,因为O、D、P0、P1、P2都是三维向量,有三个参数,所以有三个式子,因此可以解出未知的三个参数,这样就可以直接与三角形求交,不用和面求交
但是,这依然很慢,当模型越精细,面数就越多三角行也越多
光线与表面(三角形)求交加速
Bounding Volumes
我们如何进行求交加速呢?可以用包围盒
包围盒是包裹物体的盒子,可以理解为三个对面形成的交集

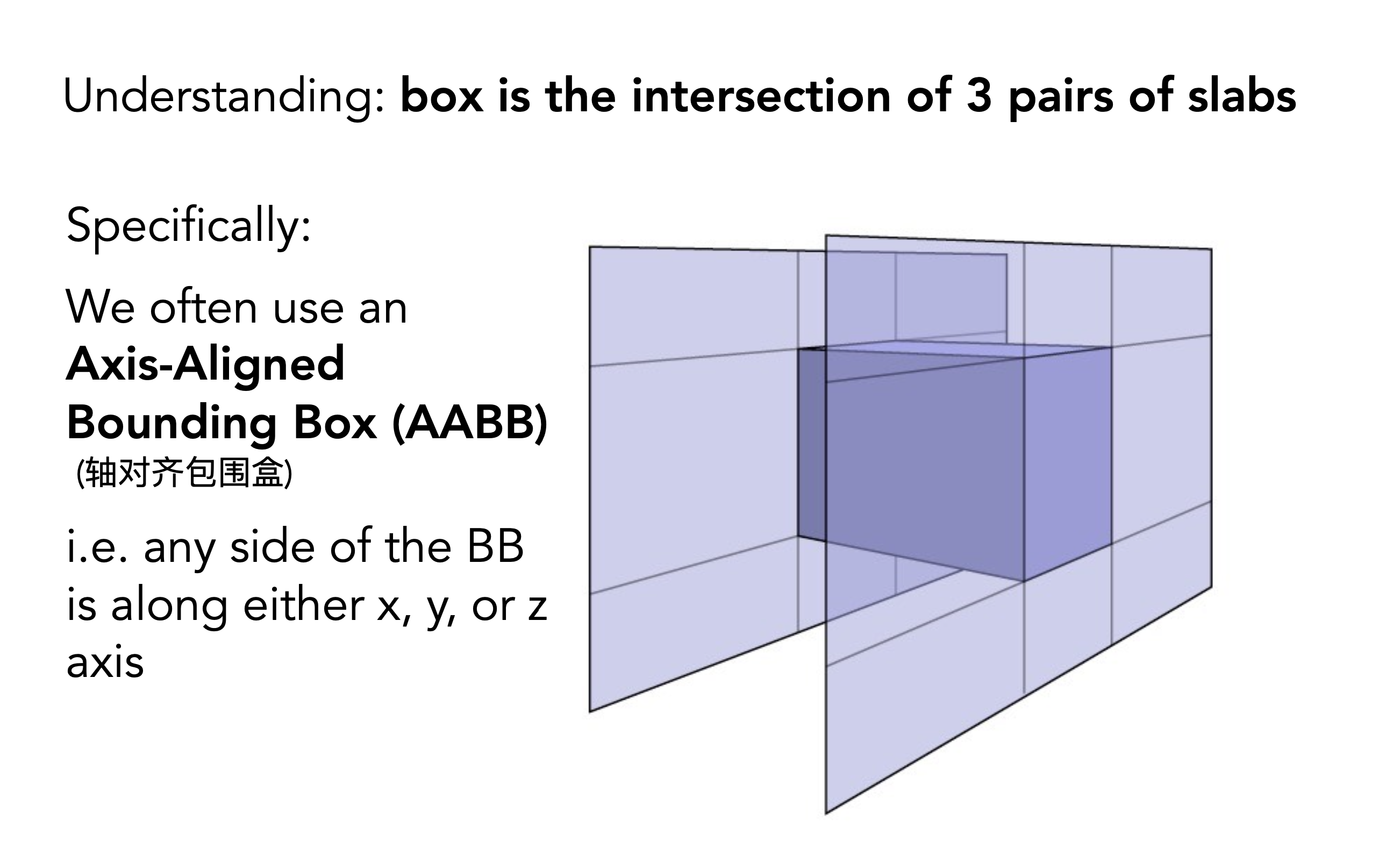
我们可以判断光线与物体的这三个对面的求交,来决定要不要和场景中的物体中的三角形求交,减少物体数量就可以减少三角形数量
我们以光线进入这三个对面的时间点来判断
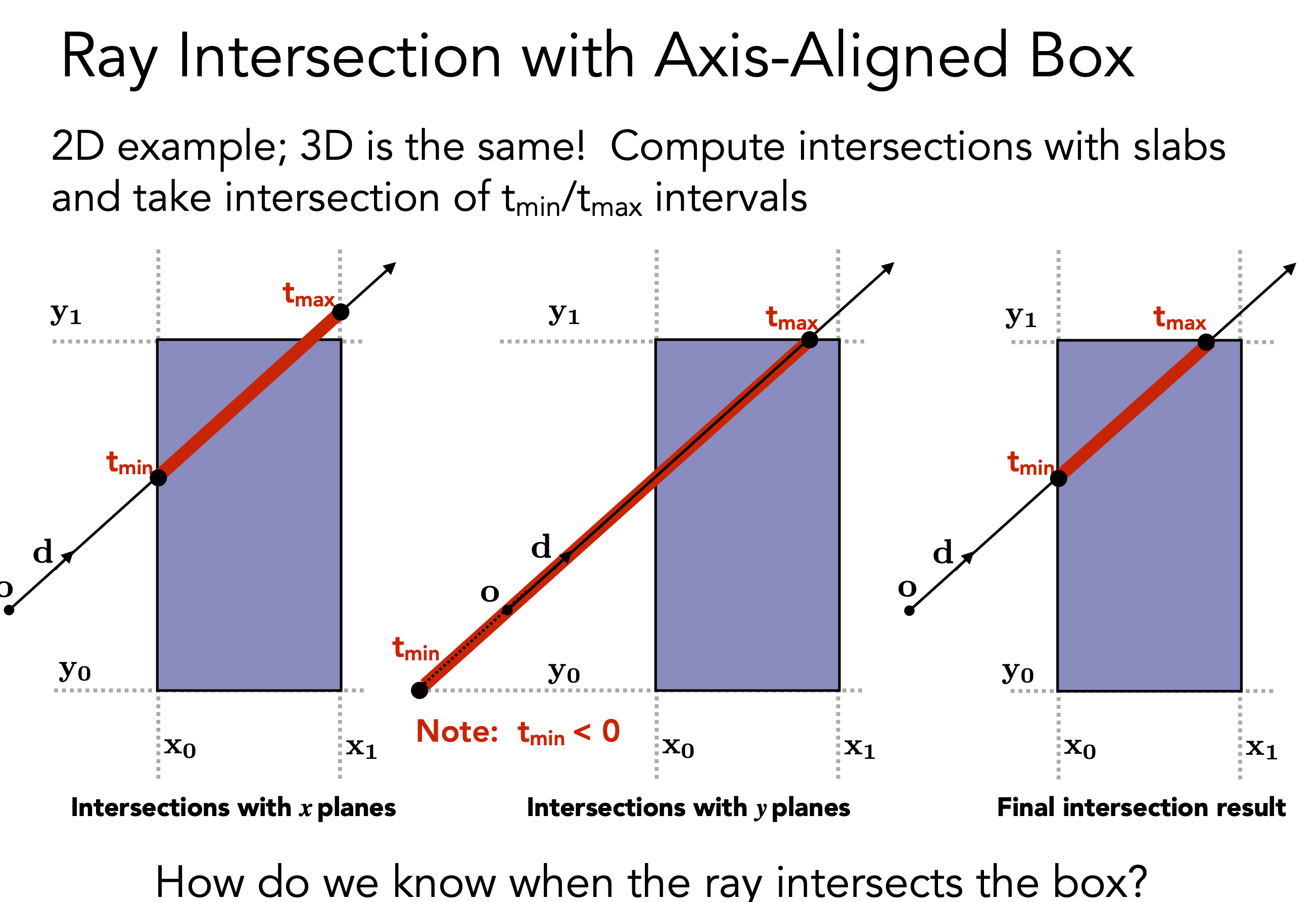
与三个对面中的每个对面都求出它们的进入的时间(最小的时间),出去的时间(最大的时间)
获得三组的进入和出去的时间后,我们取最大的进入时间,取最小的出去时间,这段时间就是三个对面的交集,也就是光线真正进入和离开物体的时间

关键点逻辑解释:
当光线都进入了三个对面,才进入盒子,所以取最大的进入时间
当光线离开一个对面,就离开了这个盒子,所以取最小的出去时间

因此有以下关系:
光线离开时间 < 0,光线在盒子背后
光线离开时间>=0同时进入时间<0,光线在盒子内部发出来的
光线进入时间小于光线离开时间,同时离开时间>0,光线从外部进入盒子一段时间后离开
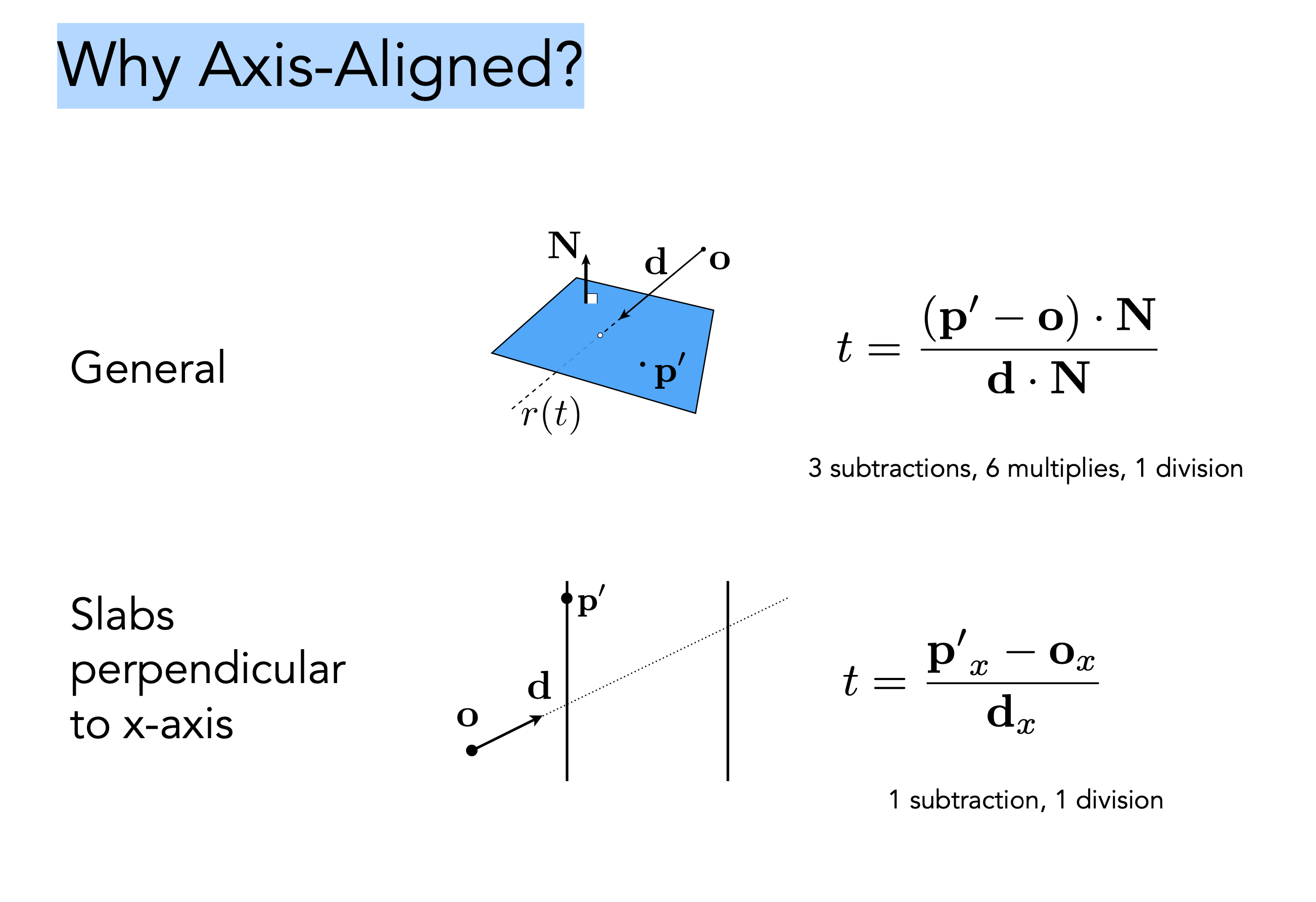
为什么要用和坐标轴平行的面来做包围盒?
因为求不同面的t,只要用对应面的轴分量减去光线对应轴的分量就可以很简单的求出来对应的t值,这样计算方便简单,相比较于与平面求交求t
空间划分
我们用AABB来包围物体来与光线求交,那也可以用AABB来加速光线和场景求交的问题,来找到空间中的物体
1.均匀的格子(早期空间划分的尝试,现在依然在一些地方使用很合适)
我们先找到一个场景,把场景的包围盒找出来,把包围盒划分成一个个格子,再找出与物体表面相交的格子
当光线从某个点发射,可能会先和某个场景盒子相交,如果和某个场景盒子相交,就有可能和盒子里的格子相交,再判断与哪些格子相交,相交的格子内部有没有物体,如果有物体再判断和物体求交
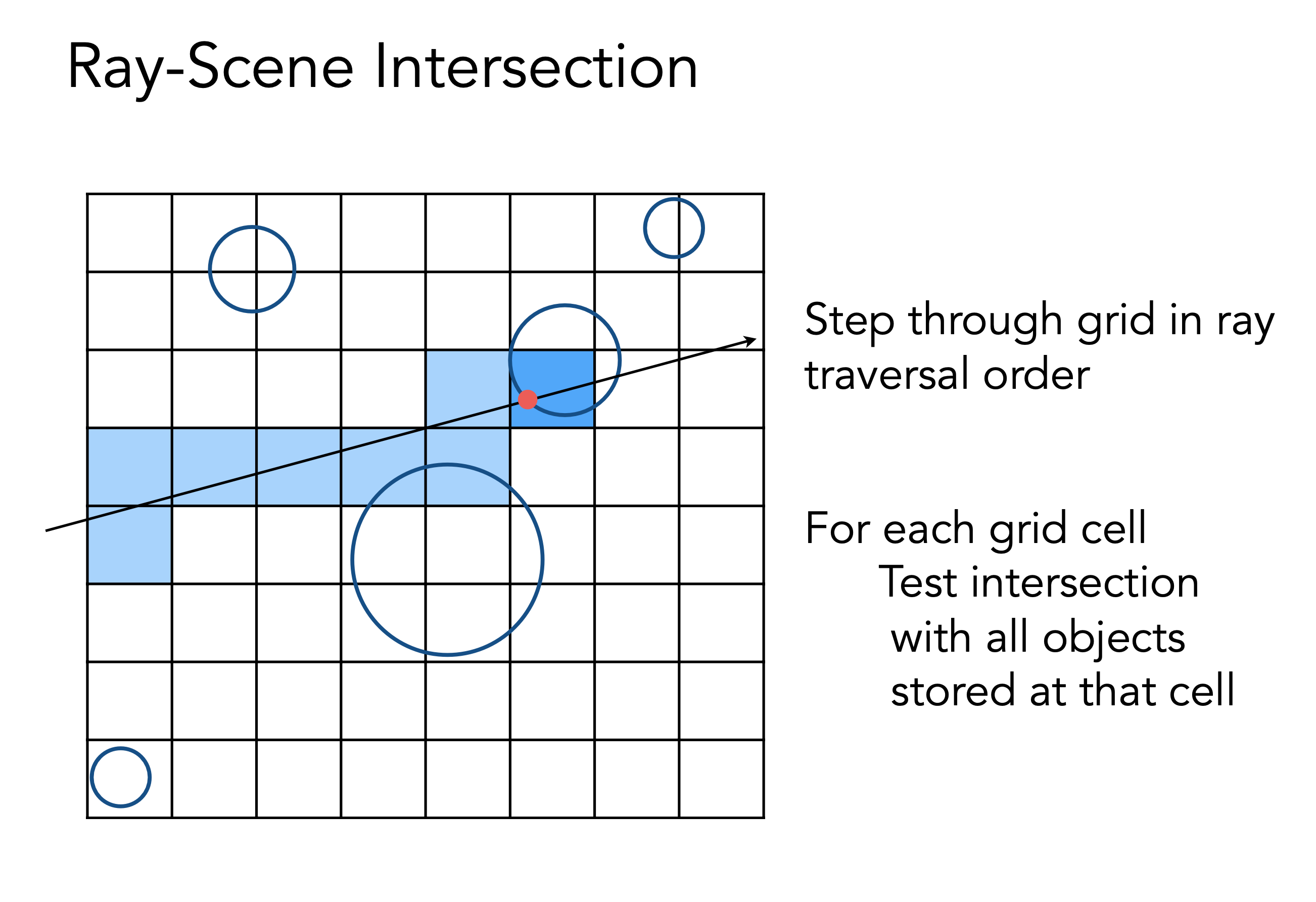
与多少数量的格子求交也会影响判断的效率,所以有一个通用的数量来做这个加速
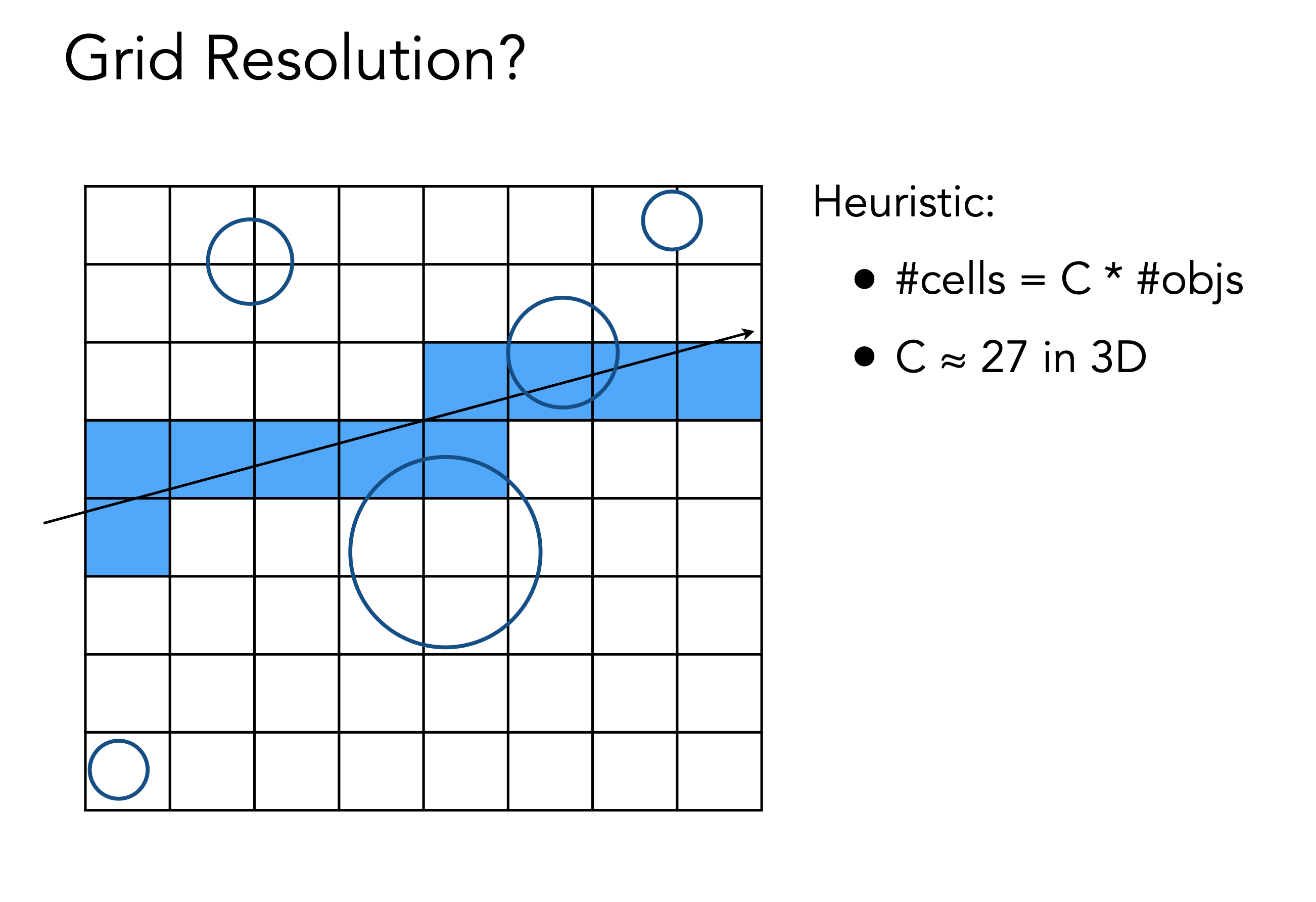
这种方法对于场景中物体均匀放置时非常有效的,但是如果场景中的物体很少,空白区域很大效率就很低


因此有后来的空间划分来解决这个问题
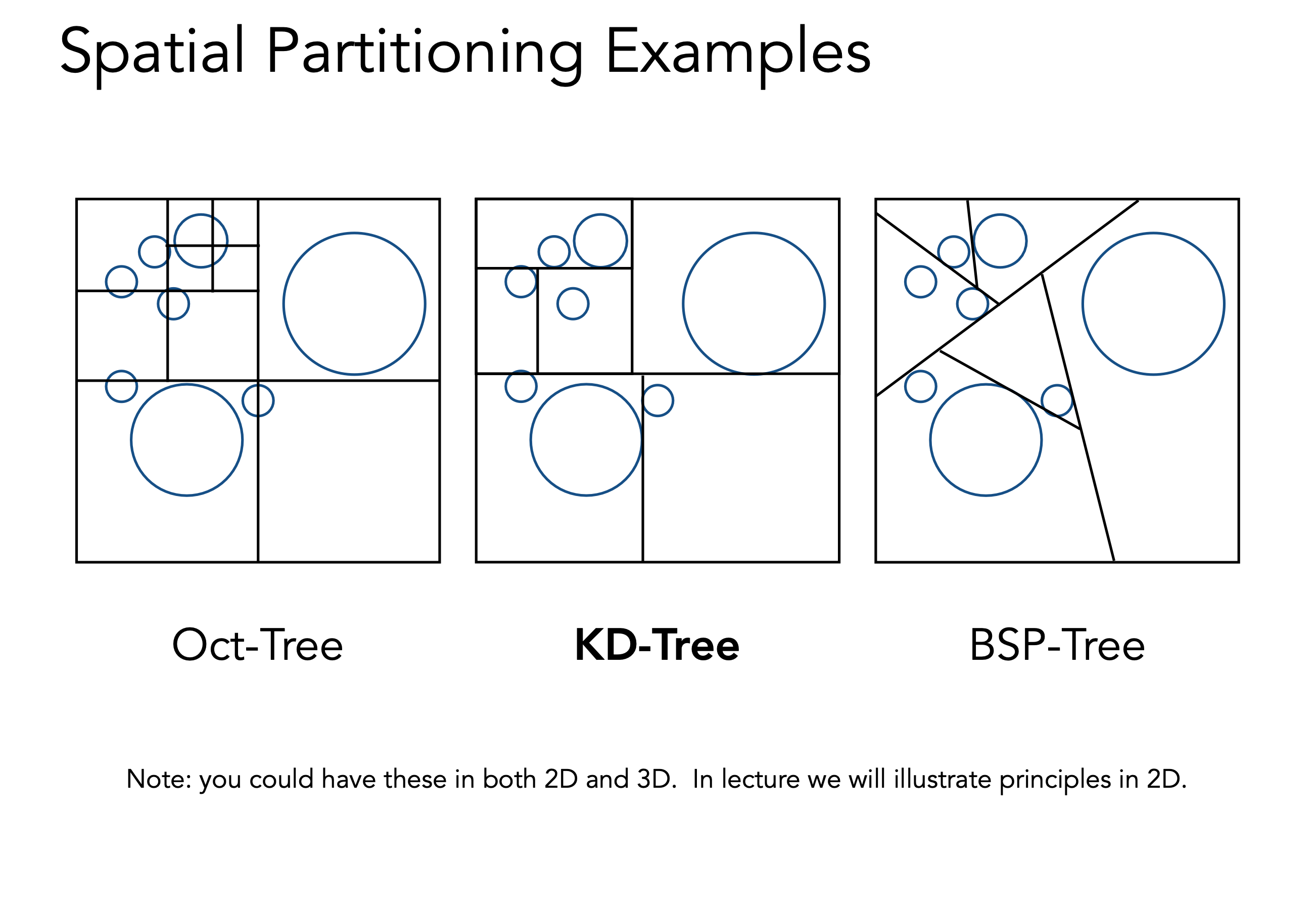
KD-Tree使用数据结构树来划分场景,没一个场景划分成两个空间,每个空间再根据物体再划分成两个,作为这个空间的子空间,递归下去,一直到最后的子空间没有物体可以再划分
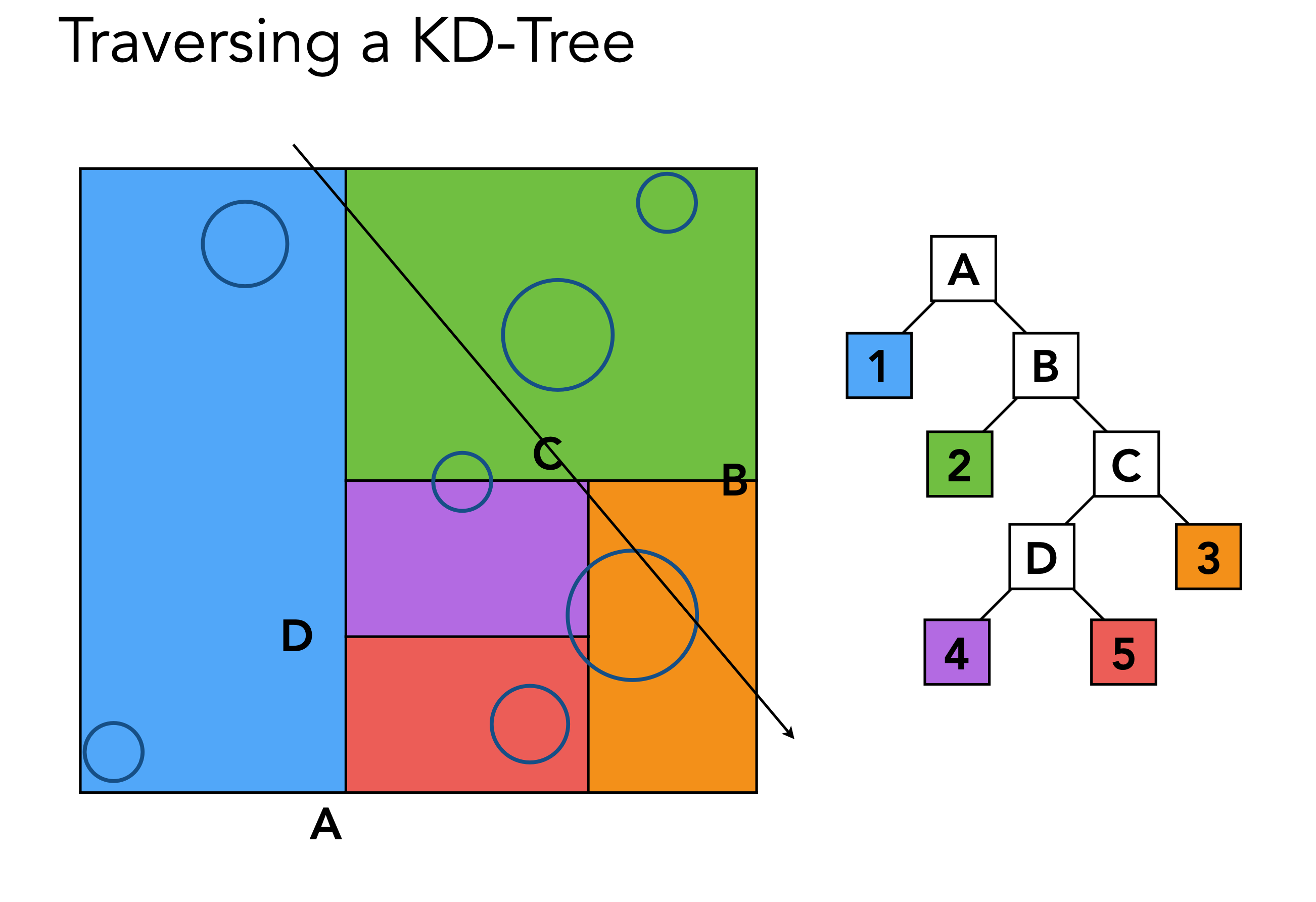
光线从场景外侧进来,首先和最上方的节点求交,如果和节点有交点,再和节点的子节点求交,如果没有子节点了,就喝节点内部的物体求交,如此循坏递归下去,直到出了场景最下方的节点
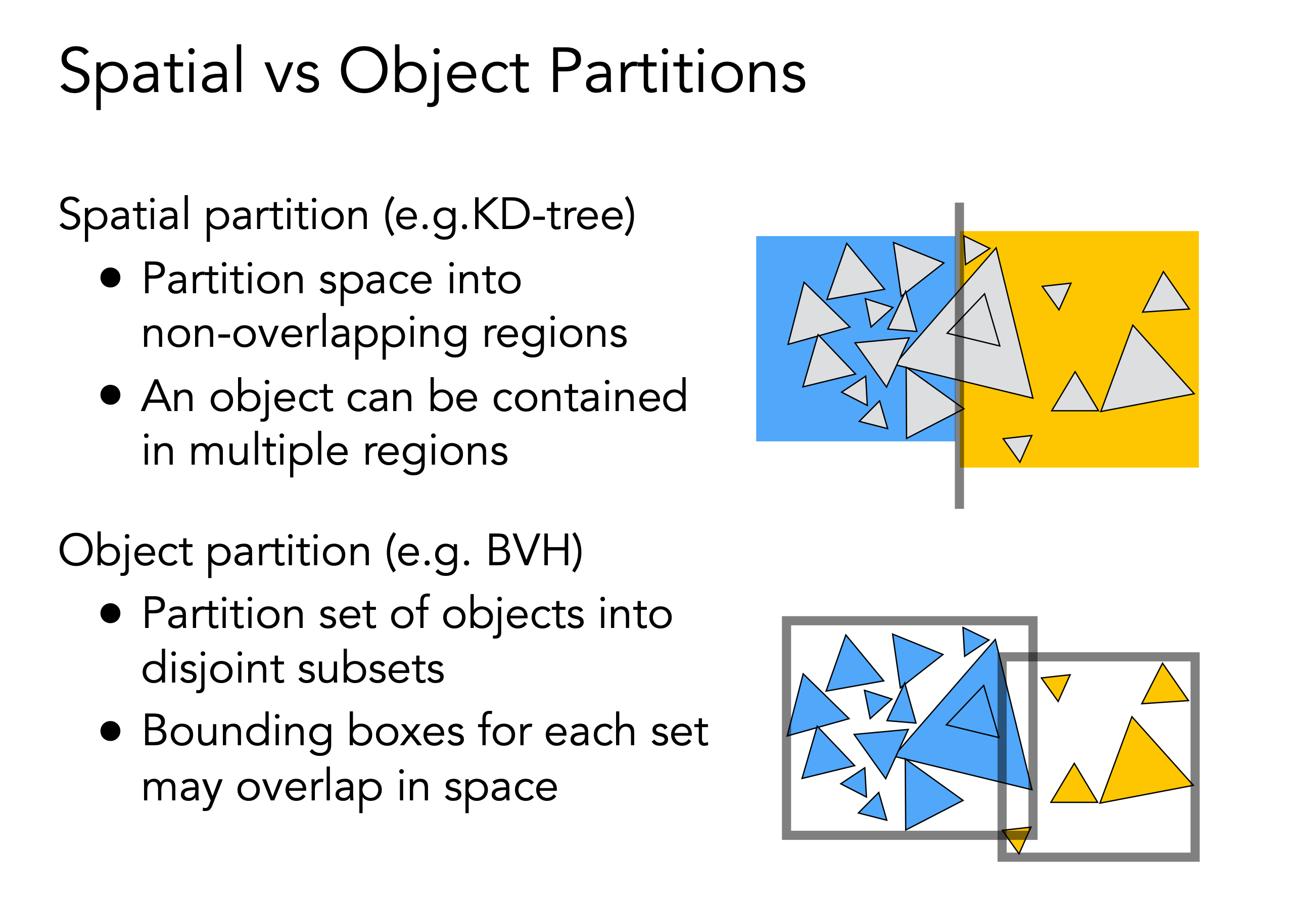
但是,如何判定三角行与场景包围盒有交点?这个问题很难准确的解决,因为场景的物体其实都是有三角形构成,而与三角形的相交判定非常难,虽然有算法,但是不准确。另外KD-Tree划分空间,会有一个物体同时出现在不同的子节点,这样多重复不直观,人们不希望出现这样麻烦的情况
所以出现另外一种更加有效的划分方法,目前几乎都在使用的方法,物体空间划分
Bounding Volume Hierarchy (BVH)
划分方法:
1.沿着最长的轴划分,保证划分的上下左右的物体比较均衡
2.找中间的三角形划分,保证划分的左右三角形数量比较均衡,取三角形的重心,沿x轴排序,可以用快速选择算法找出中间的物体,直到划分后的空间物体小于N(自己定义,例如5)个后停止划分
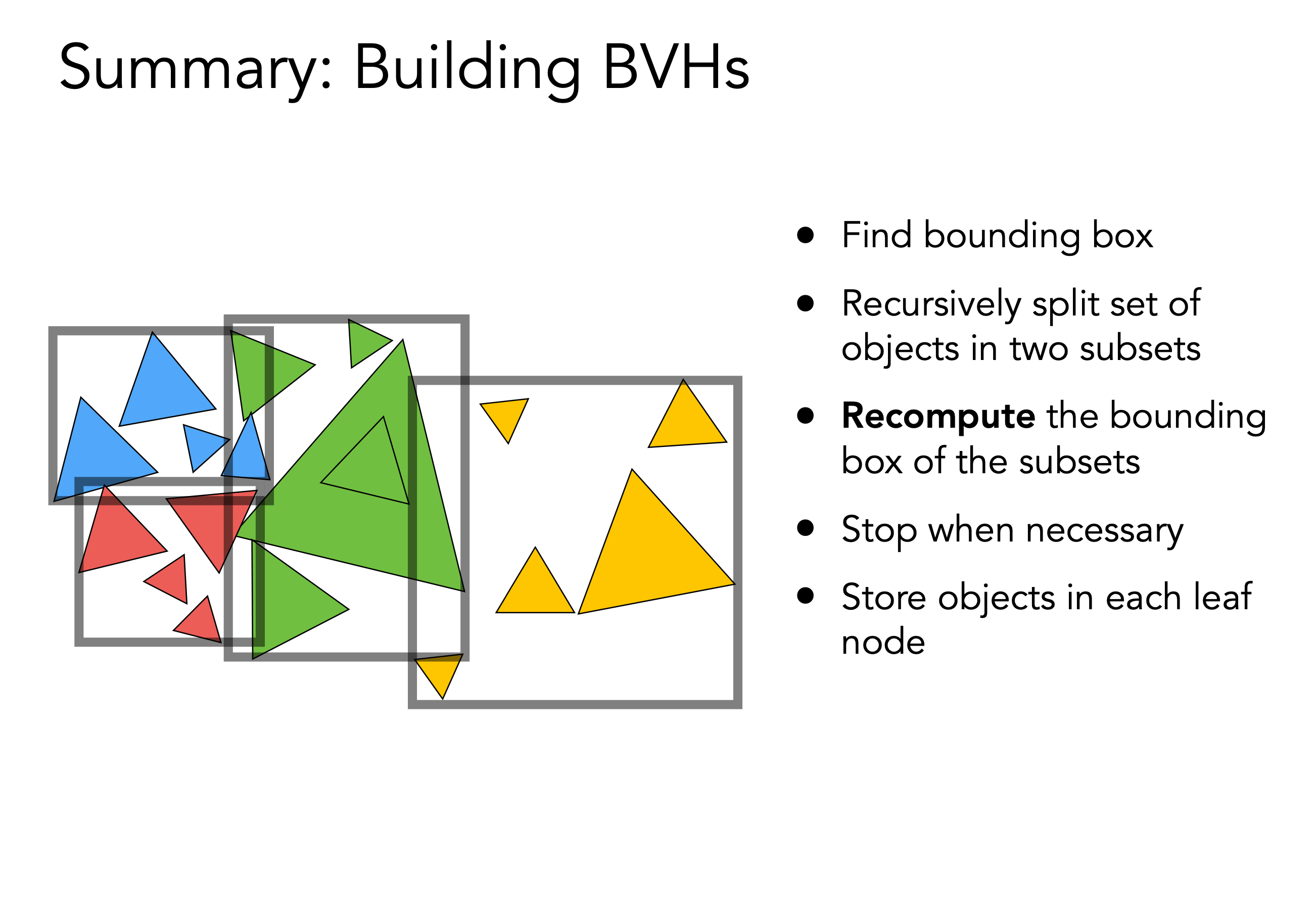
光线与BVH求交算法伪代码
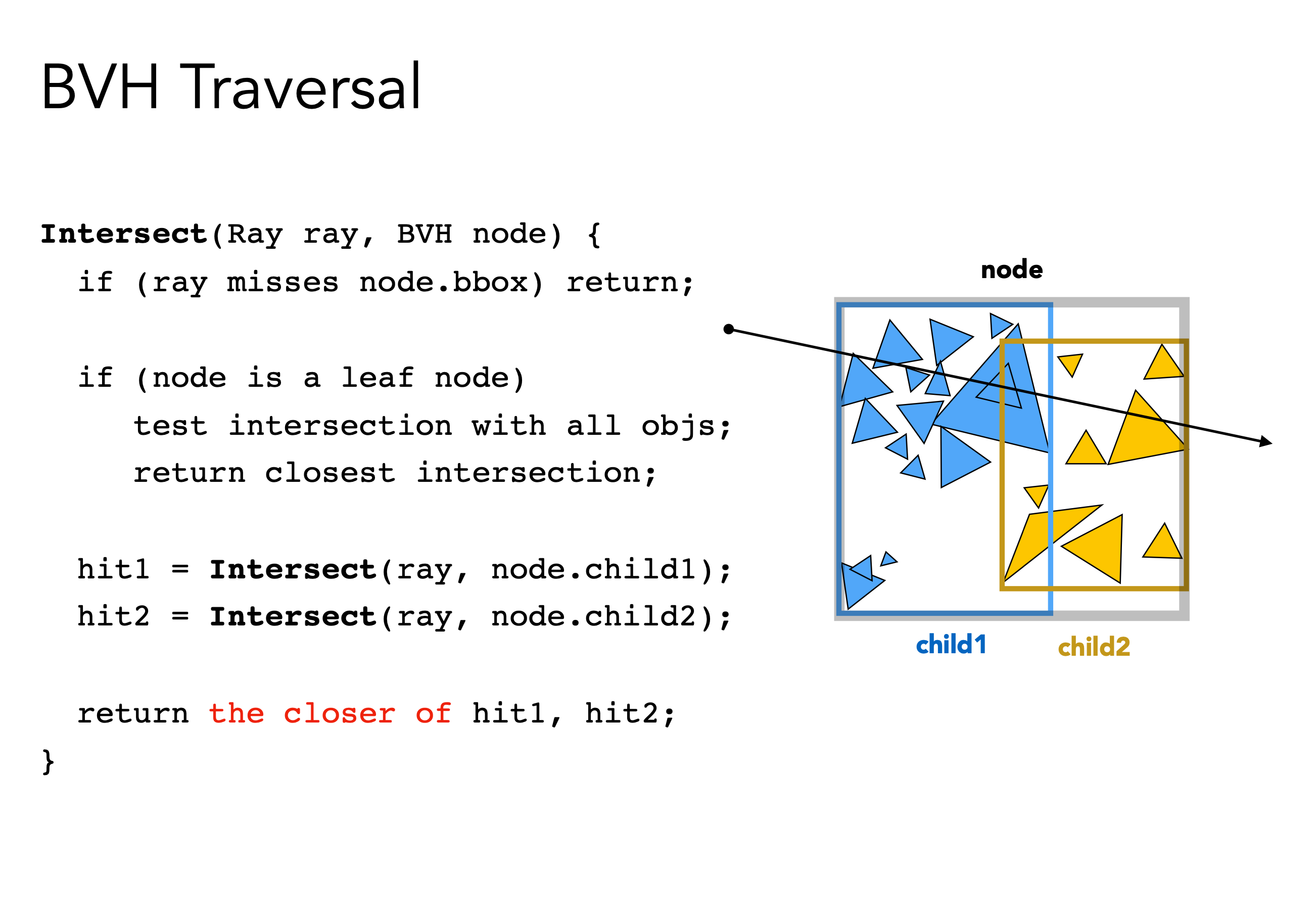
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
Intersection BVHAccel::Intersect(const Ray& ray) const
{
Intersection isect;
if (!root)
return isect;
isect = BVHAccel::getIntersection(root, ray);
return isect;
}
Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
Vector3f invDir = Vector3f(1.0f / ray.direction.x, 1.0f/ ray.direction.y, 1.0f/ray.direction.z);
std::array<int, 3> dirIsNeg = {
(int)(ray.direction.x > 0),
(int)(ray.direction.y > 0),
(int)(ray.direction.z > 0)
};
// TODO Traverse the BVH to find intersection
if (!node->bounds.IntersectP(ray,ray.direction_inv,dirIsNeg))
{
return Intersection();
}
if (node->left == nullptr && node->right == nullptr)
{
return node->object->getIntersection(ray);
}
auto hit1 = getIntersection(node->left,ray);
auto hit2 = getIntersection(node->right,ray);
return hit1.distance < hit2.distance ? hit1 : hit2;
}
inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
const std::array<int, 3>& dirIsNeg) const
{
// invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z), use this because Multiply is faster that Division
// dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)], use this to simplify your logic
// TODO test if ray bound intersects
float tMax_x = (pMax.x - ray.origin.x) * invDir.x;
float tMin_x = (pMin.x - ray.origin.x) * invDir.x;
float tMax_y = (pMax.y - ray.origin.y) * invDir.y;
float tMin_y = (pMin.y - ray.origin.y) * invDir.y;
float tMax_z = (pMax.z - ray.origin.z) * invDir.z;
float tMin_z = (pMin.z - ray.origin.z) * invDir.z;
if (!dirIsNeg[0])
{
float t = tMin_x;
tMin_x = tMax_x;
tMax_x = t;
}
if (!dirIsNeg[1])
{
float t = tMin_y;
tMin_y = tMax_y;
tMax_y = t;
}
if (!dirIsNeg[2])
{
float t = tMin_z;
tMin_z = tMax_z;
tMax_z = t;
}
float tExit = std::min(tMax_x, std::min(tMax_y,tMax_z));
float tEnter = std::max(tMin_x,std::min(tMin_y,tMin_z));
if((tEnter <= tExit) && (tExit >= 0)){
return true;
};
return false;
}
以上就是空间和物体划分的区别,这样光线与空间的求交就可以很快完成
Basic radiometry (辐射度量学)
之前的光照模型中,光的强度10并没有单位,是假设的。如果要还原真实的光照强度,我们需要知道真实世界中光精准的度量单位
Radiant Energy
光源辐射出的能量,单位焦耳
\(Q [J = Joule]\) Radiant flux (power)
单位时间上的能量,单位瓦特
考虑时间上的能量,时间越长,接受的能量就越多就越热 \(\Phi \equiv dQ [W = Watt] [lm = lumen]*\)
Radiant Intensity
单位立体角上的能量
单位立体角就是单位面积除以距离平方 \(I(\omega) \equiv d\Phi / d\omega\)
Angles and Solid Angles
立体角,在三维空间中某个球面的面积除以面积距离球心距离的平方 \(\omega = A/r^2\) 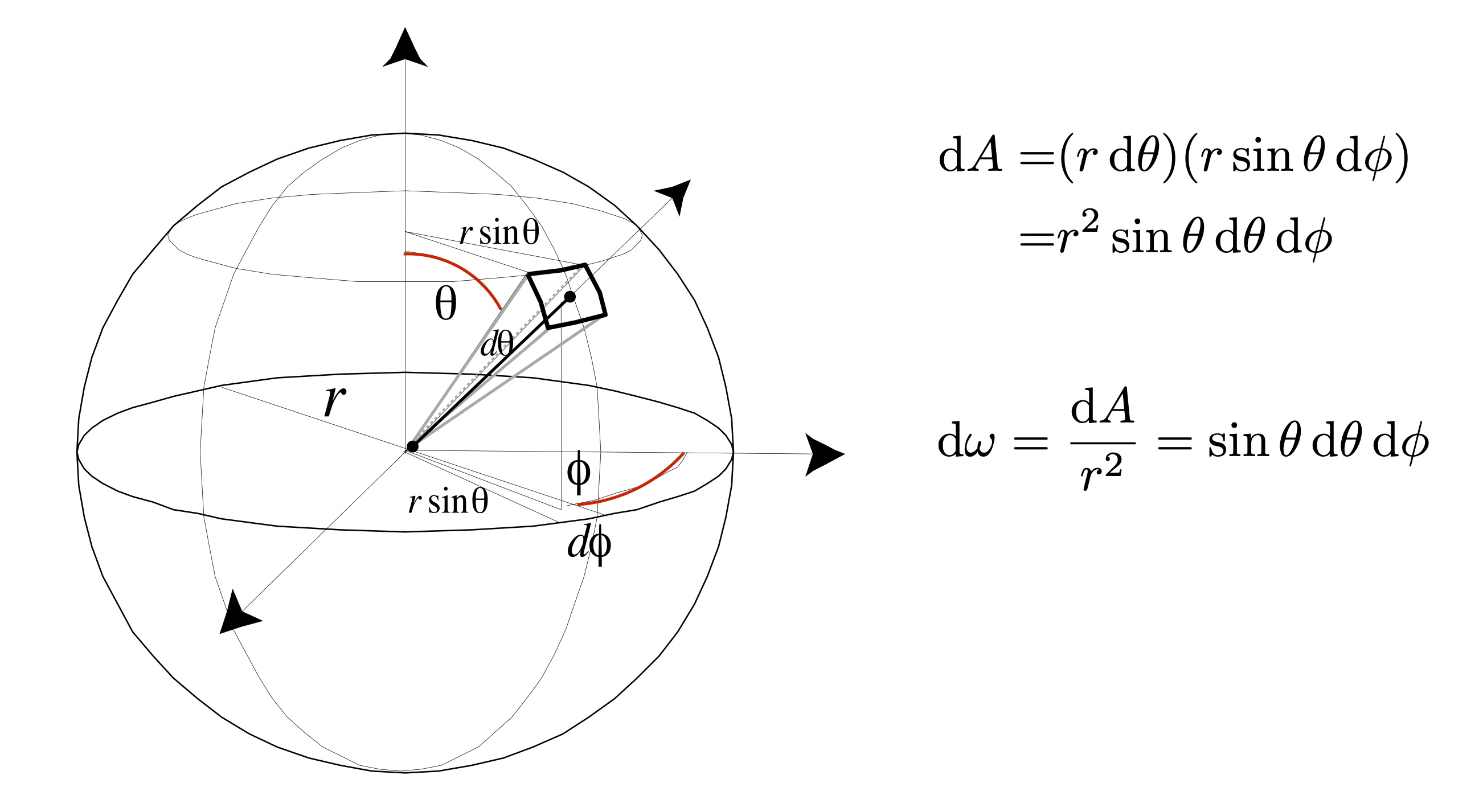
Irradiance (power per unit area)
单位时间面积收到的能量(所有方向的光),必须是投影后垂直于面积的光的能量 \(E(x) \equiv d \Phi(x) /dA\) 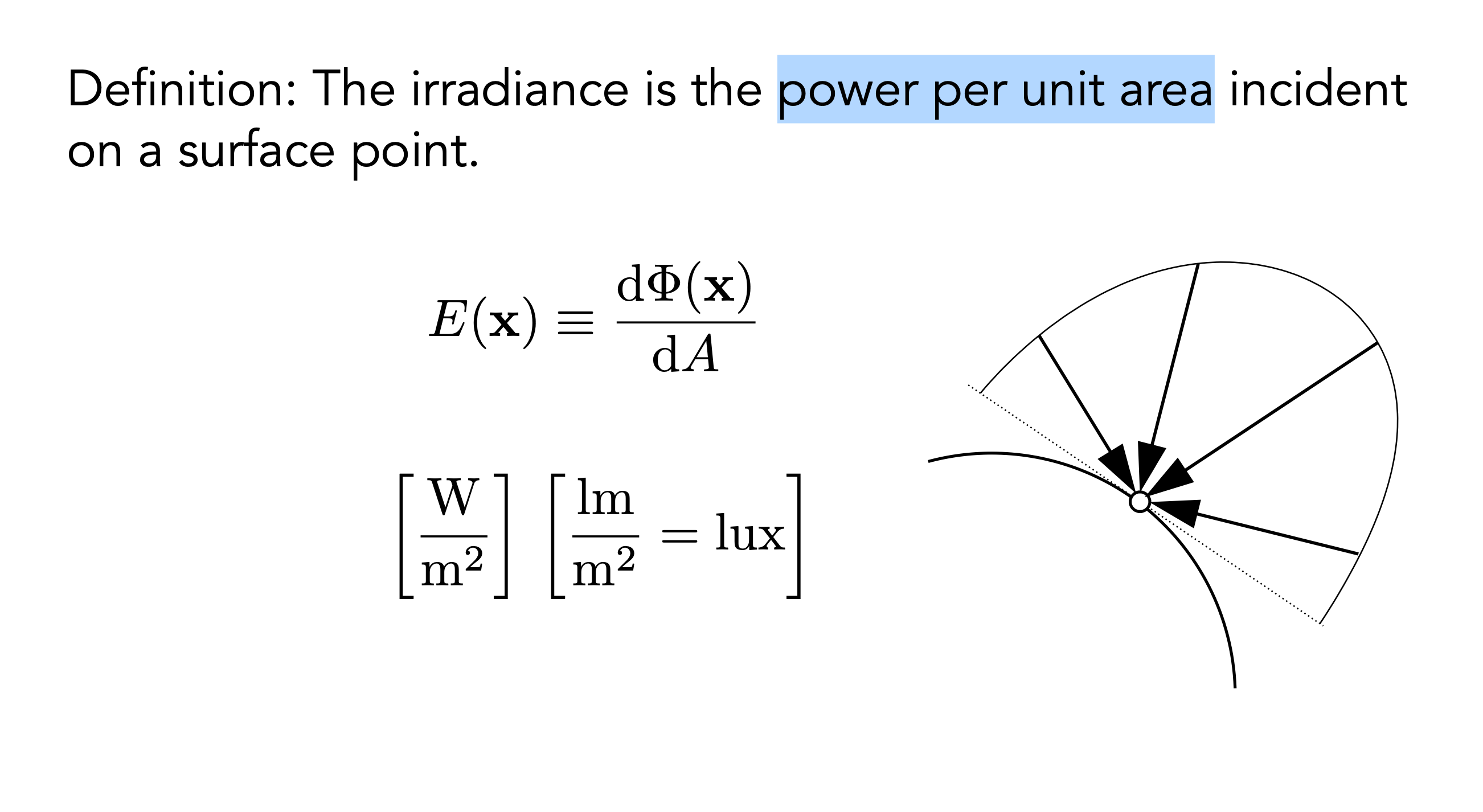
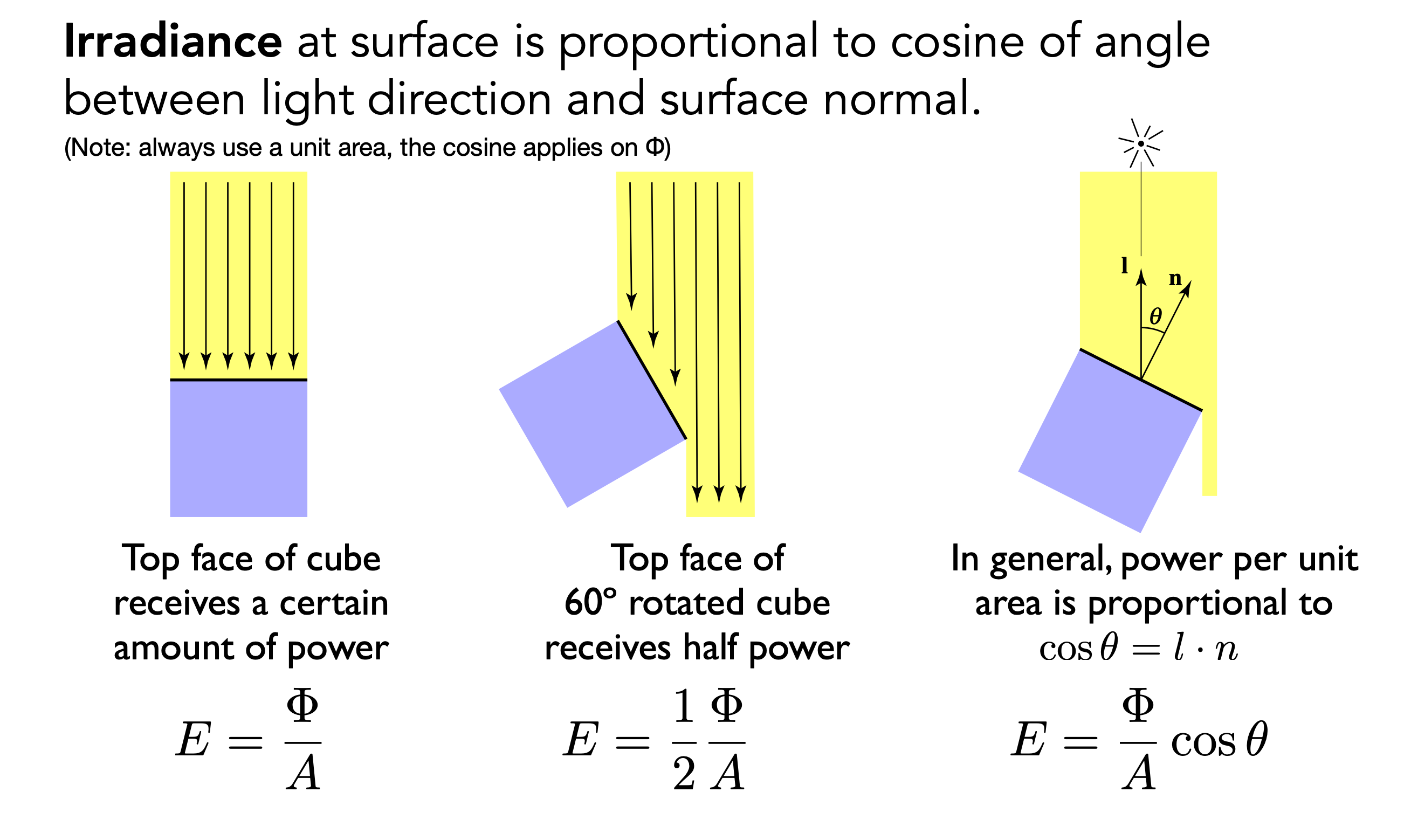
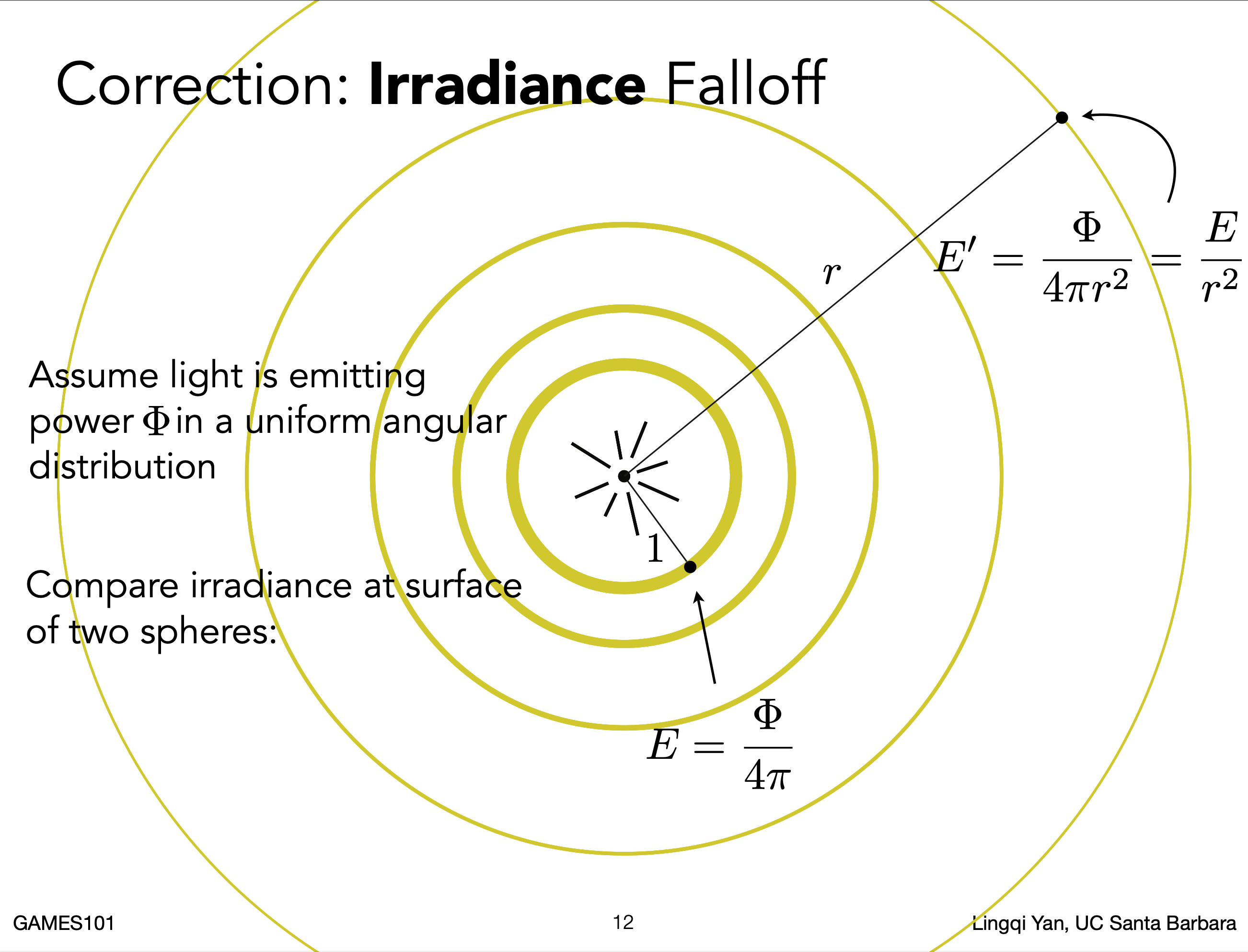
Irradiance用来定义随时间变化,单位面积上的能量的衰减,而Radiant Intensity随时间变化对应的能量是没有衰减的
Radiance (per unit solid angle, per projected unit area)
单位立体角、单位投影面积上的能量,有两种场景
Incident Radiance
某一个单位面积收到的某一个方向进来的能量

Exiting Radiance
某一个单位面积往某一个单位立体角上发射出去的能量

Irradiance和Radiance的关系
求某块面积收到的能量就是对所有可能过来的方向的光的的能量进行积分求和,Irradiance其实就是所有的Radiance积分求和
BRDF 光反射方程
在某一小块面积上收到从某个方向进来的光, 如何计算它往四面八方某一个方向反射出去
计算不同材质收到的光往各个方向分配,如漫反射、镜面反射,BRDF就可以定义如何去分配
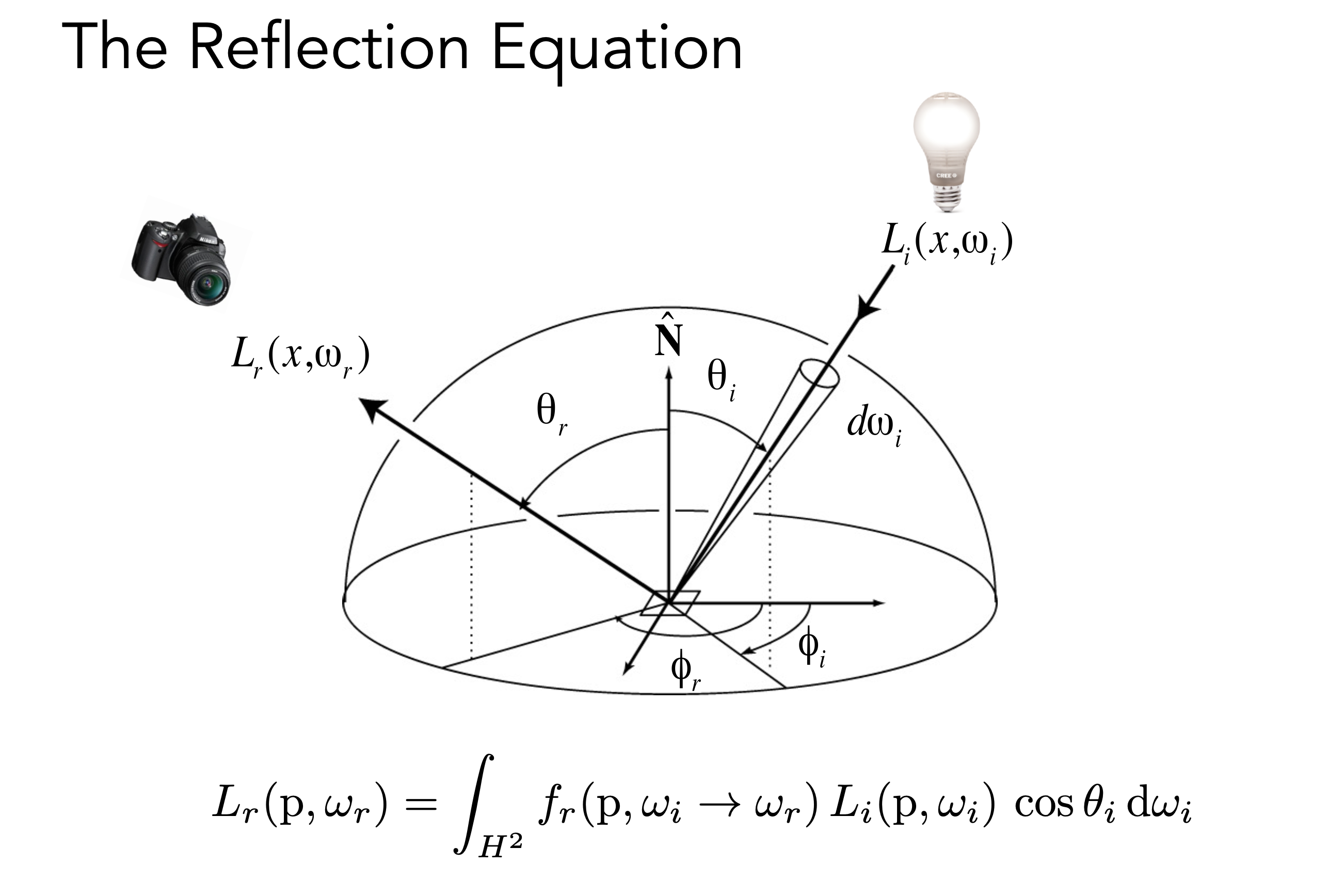

渲染方程经过简化,具体过程可看视频推导过程
L 物体所有辐射出来的能量
E 光源辐射出来的能量
K 物体所有辐射出来的能量经过BRDF反射出来的能量

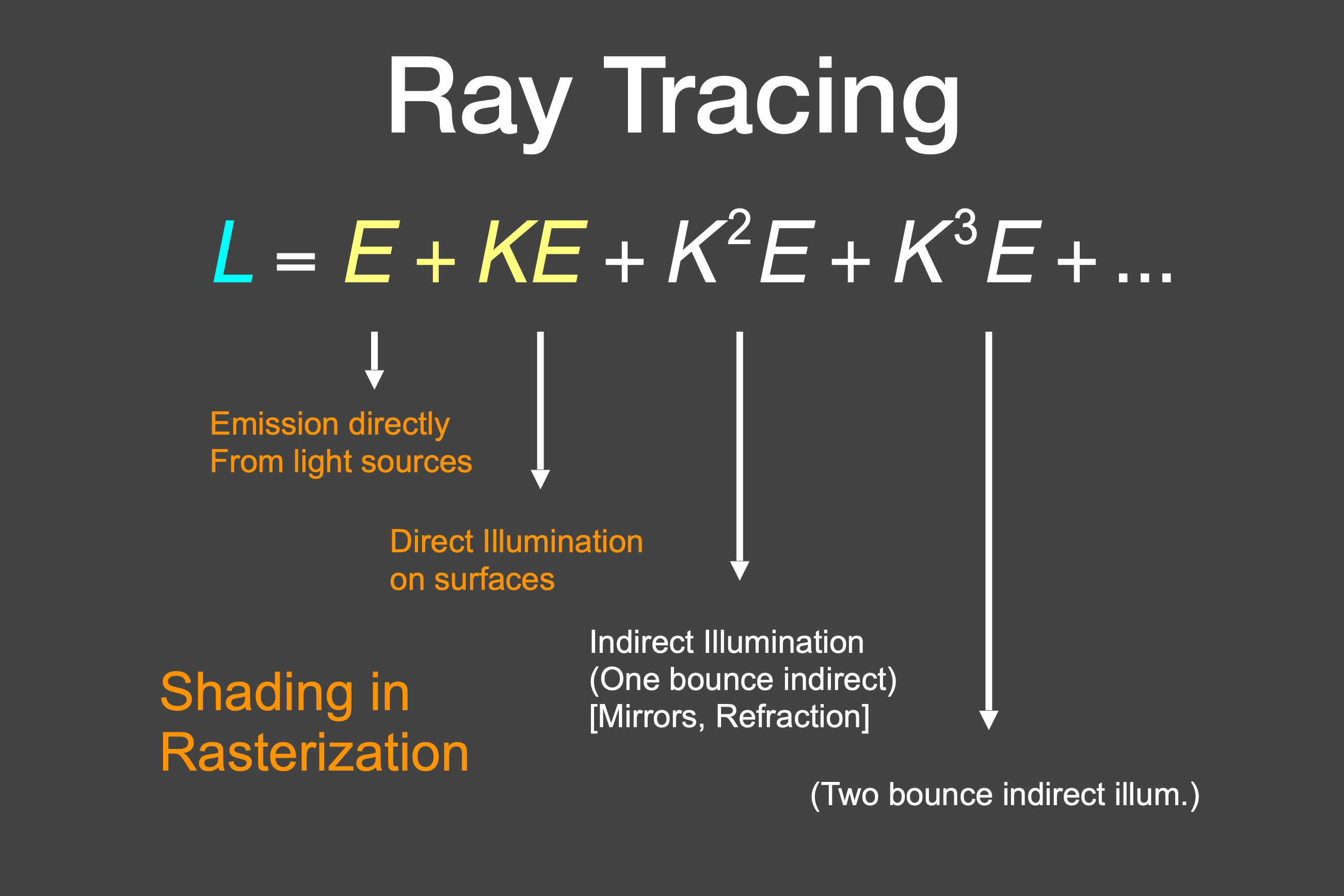
E 光源发射出来的能量
KE 一次反射
k2E 两次反射
光栅化中只有前两部分,后面部分是光栅化比较麻烦处理的内容:
E 光源
KE 直接光照
光线追踪可以很容易解决光线传播后面的部分,全局光照
光线追踪需要用到概率论的知识:
Probability Distribution Function (PDF)
概率密度函数
随机取一个随机变量,代入概率密度函数取得的积分面积就是取得的概率
 期望
期望
变量乘概率密度积分起来
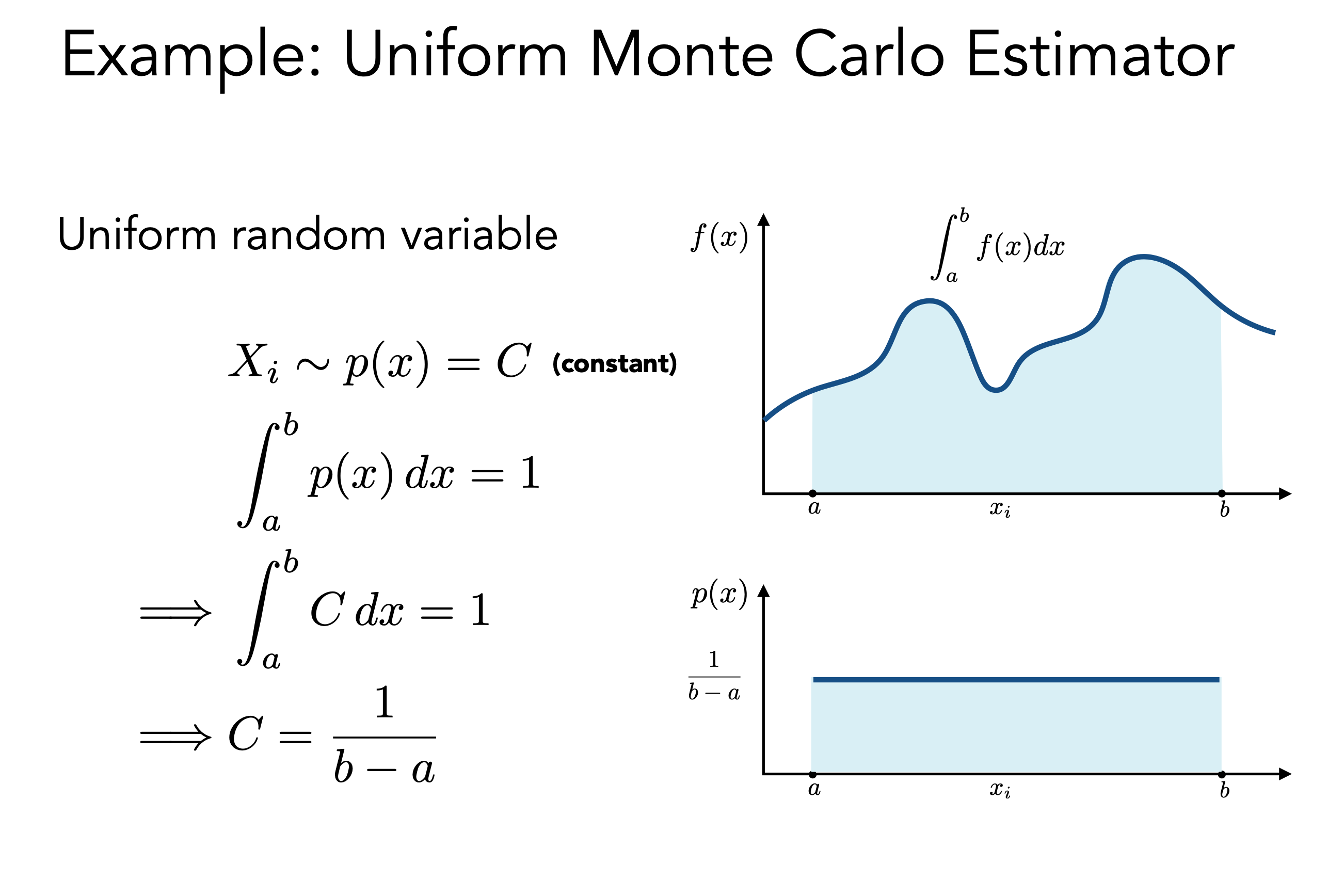
Monte Carlo Integration
将无数微小的面积采样然后积分起来再求平均,就可以求的不规则函数的面积
求得的PDF为 1/ b-a

Path Tracing
首先因为场景中物体出了光源,自身都不发光,所以我们将渲染方程中的自发光项去掉,只考虑反射,称为反射方程

方程就是在半球上不同方向上的积分,我们可以用蒙特卡罗积分来解这个问题
选一个着色点,随机选一个方向,就是我们的随机变量X,需要求出f(x)和PDF
f(x)就是方程
PDF就是半球表面积分之一,球面面积是4pi,半球面积是2pi,半球上某个方向立体角就是1/2pi

根据蒙特卡罗积分就可以将方程转化为如下求和式

现在可以开始写算法
以下是一次光照

递归就是全局光照

但是光线数量会指数级暴增,因为递归一次是随机选择N个方向采样
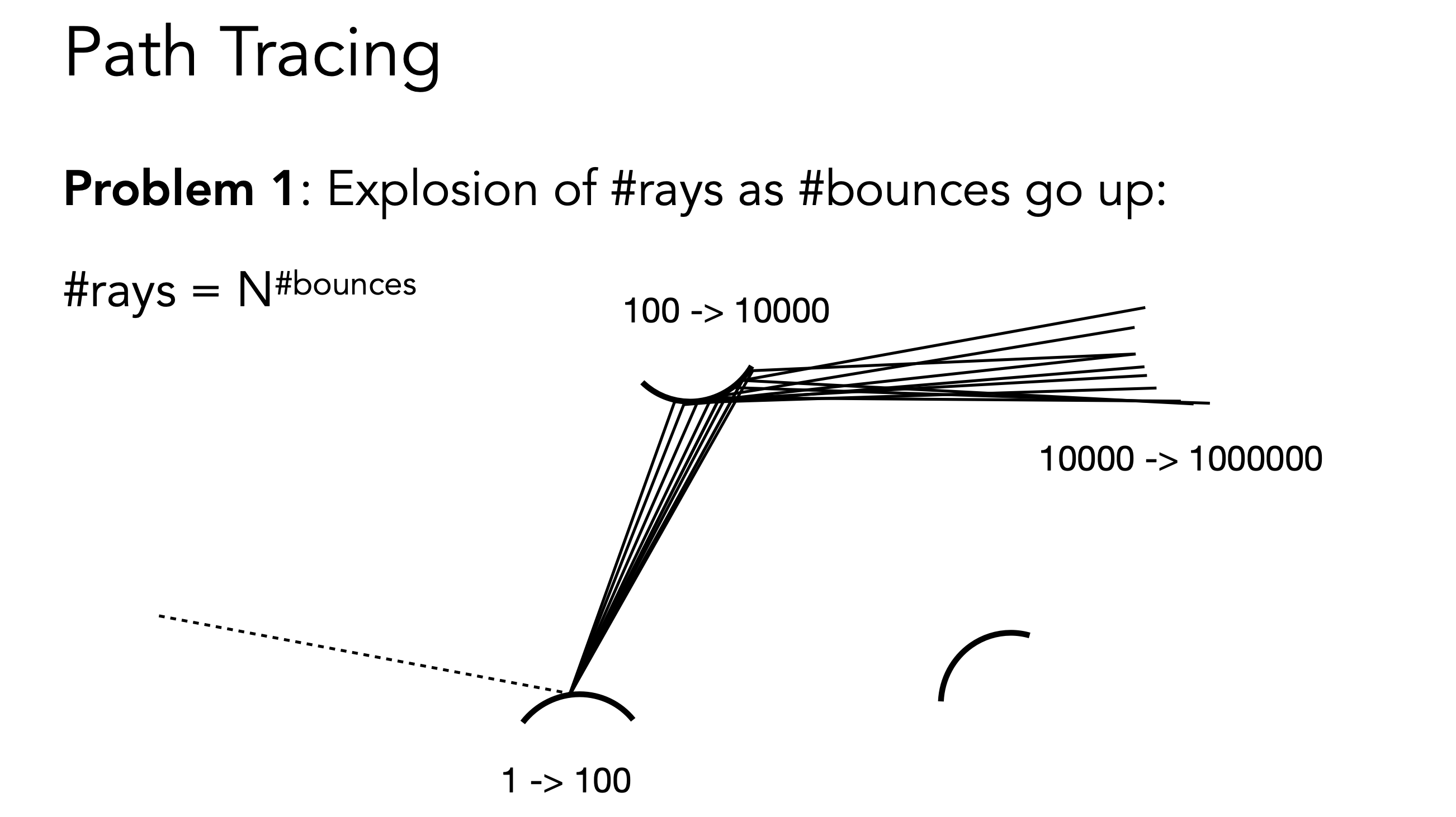
光线追踪是路径追踪,路径是指很多不同的单一路径,所以只发射一次

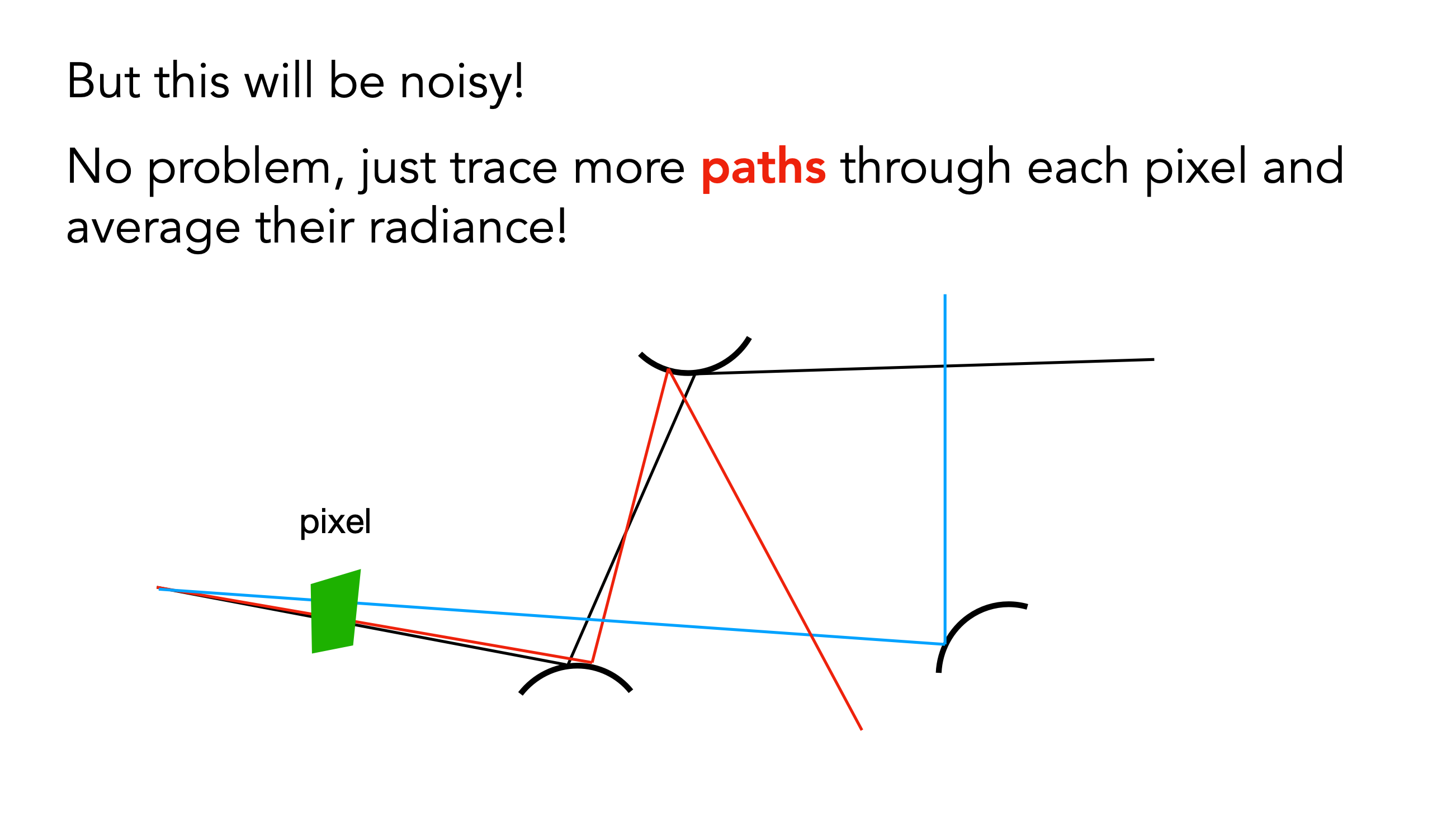
增加停止条件,如果射中了物体,继续递归,如果射中了光源,停止递归

但是真实世界中光线弹射是不会停止的,这样做会减少光线的弹射次数,会让场景损失很多能量
光线弹射三次场景亮度

光线弹射十七次场景亮度

Russian Roulette (RR)
限制弹射次数是不对,所以我们可以用俄罗斯轮盘赌来解决这个问题
俄罗斯轮盘赌的游戏中,左轮手一共可以装 6发子弹,我们装上4发子弹,然后开枪,有4/6的概率被射中,2/6的概率不射中活下来,我们可以用我们希望的概率来发射光线

我们以一定的概率P往外发射一条光线,1-p的概率不发射光线,期望公式如上,概率乘于着色结果再除以概率,加上一减概率乘于没有追踪的结果零,如果命中概率就得到我们期望的着色值,如果没命中,就没有着色值,刚好获得我们需要的着色结果,因为总的获得光线能量的概率总和不超过1,分布是平均的,我们只需要设定一个合理的期望的概率

算法如上,随机取值,如果小于于我们的概率,发射一条光线,获得结果后除以概率获得我们的期望结果
这就是一个完整的算法了!但是!还有一点小问题,因为我们是随机方向发射,场景中物体大小决定了有多大概率光线能击中物体(包括光源),物体大被击中采样的概率大,物体小采样概率就小,有更多光线被浪费掉了,因此造成低采样率画面就会有噪声,高采样率就会比较干净,那么如何在低采样率下也能得到干净画面?

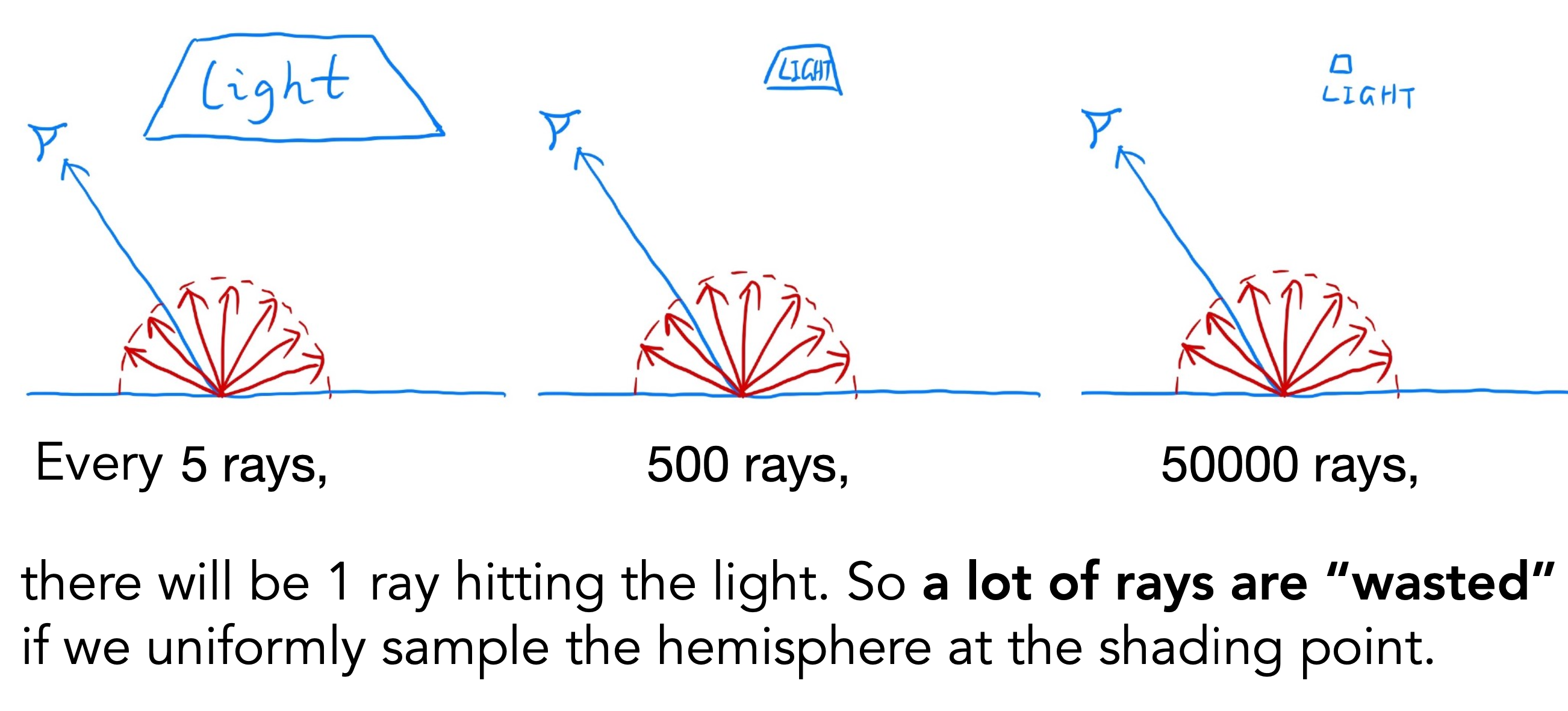
因此我们可以直接对光源采样,但是渲染方程是定义在立体角球面上的,我们想要对光源采样,可以将光源面积投影,dA光源一小块面积,dw球面一小块面积,dA投影到dw就有以下公式,直接对光源采样
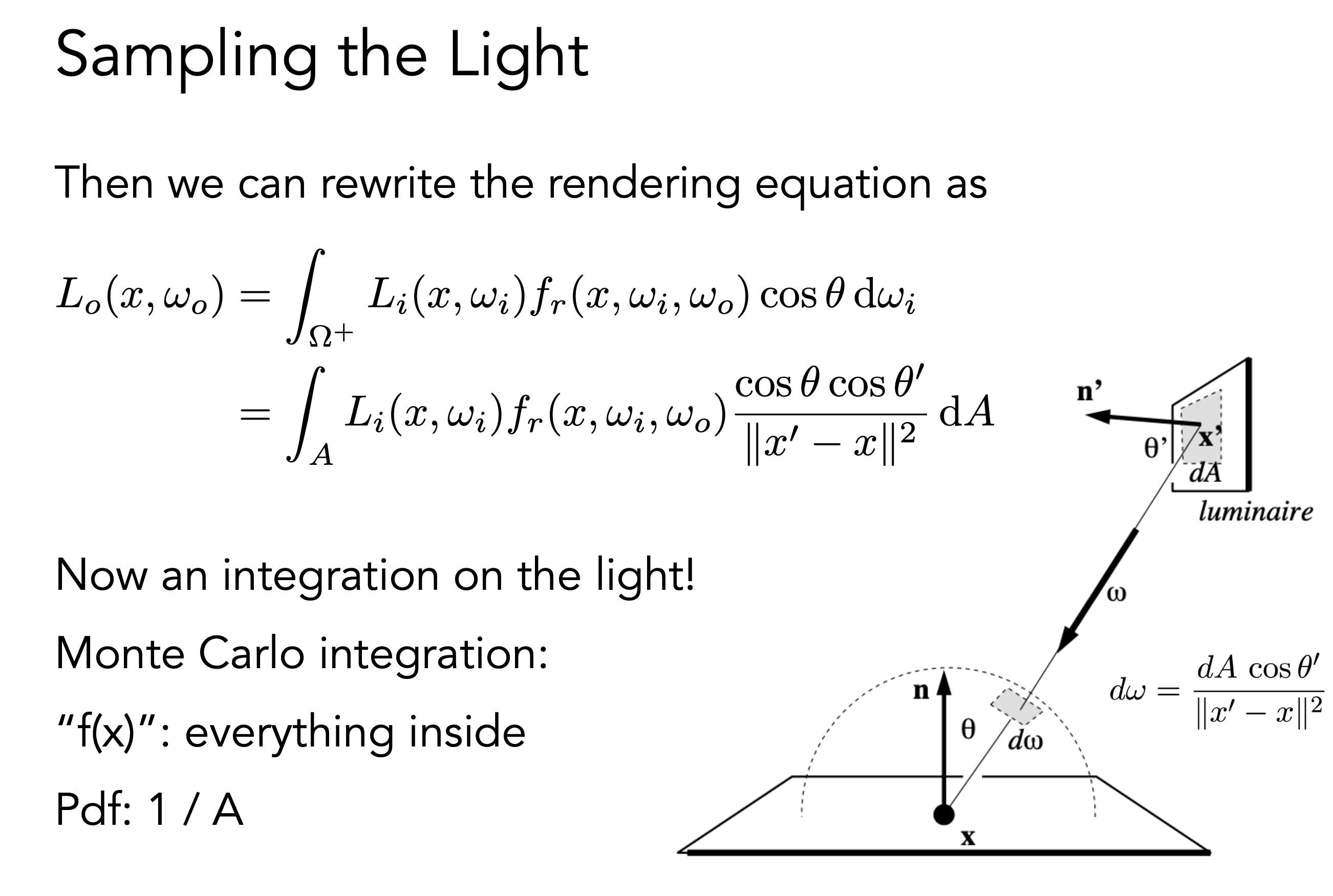
因此,来自光源的光线直接对光源采样,其他物体反射过来的光线我们还是按原来的方式随机采样,那么如何区分来自光源还是物体,哦我们只要在采样点直接连一条射线到光源,看中间是否有物体遮挡,有这事物体反射,没有就是来自光源



到这里光线追踪就算全部完成,可以看出渲染结果和照片基本无差别

最后贴下作业结果
Path Trac-ing 算法
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
// Implementation of Path Tracing
Vector3f Scene::castRay(const Ray &ray, int depth) const
{
float pdf_light;
Intersection lightInter;
sampleLight(lightInter,pdf_light);
// TO DO Implement Path Tracing Algorithm here
//ray intersction
Intersection inter = intersect(ray);
if (!inter.happened)
{
return {0,0,0};
}
if (inter.m->hasEmission())
{
return inter.m->getEmission();
}
Vector3f blockedCheckDir = lightInter.coords - inter.coords;
Intersection blockCheckInter = intersect(Ray(inter.coords,blockedCheckDir.normalized()));
Vector3f L_dir = 0.0f;
if ((blockCheckInter.coords - lightInter.coords).norm() < 0.01)
{
Vector3f L_i = lightInter.emit;
Vector3f f_r = inter.m->eval(ray.direction,blockedCheckDir.normalized(),inter.normal);
float cos_theta = dotProduct(blockedCheckDir.normalized(), inter.normal);
float cos_theta_Light = dotProduct(-blockedCheckDir.normalized(),lightInter.normal);
float point_light_distance = dotProduct(blockedCheckDir,blockedCheckDir);
L_dir = L_i * f_r * cos_theta * cos_theta_Light / point_light_distance / pdf_light;
}
Vector3f L_indir = 0.0f;
//((float)rand() / (RAND_MAX))
float randomNumber = get_random_float();
if (randomNumber < RussianRoulette)
{
Vector3f wi = inter.m->sample(ray.direction,inter.normal).normalized();
Vector3f preL_dir = castRay(Ray(inter.coords,wi),depth);
Vector3f indir_f_r = inter.m->eval(ray.direction, wi, inter.normal);
float indir_cos_theta = dotProduct(wi, inter.normal);
float indir_pdf = inter.m->pdf(ray.direction, wi, inter.normal);
L_indir = preL_dir * indir_f_r * indir_cos_theta / indir_pdf / RussianRoulette;
}
return L_dir + L_indir;
}
