资料来源:https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
Antialiasing
抗锯齿
原因:
采样出现Artfacts(不准确的现象或结果),在时域与频域上的解释是信号变化太快,以至于采样速度跟不上,用同样的采样方法,采样两种不同频率的函数信号,得出来的结果我们无法区分它,这就是频率上的走样.
解决方法:
在采样之前做模糊(低通滤波)
滤波就是去掉一系列的频率,等于平均,等于卷积.
Filtering = Convolution (= Averaging)
低通滤波,过滤掉高频信息,采样重叠的信号(Artfacts)就会被去掉,再在用稀疏的采样频率采样,就不会发生混叠,这样就进行了反走样,对应于图像就是抗锯齿.
0.滤波要涉及频域的信息,频域是信号的重复,在图形上可以就是一个函数时一系列的正余弦波的线性组合(傅立叶级数展开)

也就是时域(一个函数)可以通过傅立叶变换成频域(不同的正余弦波组合),频域也可以通过逆傅立叶变化成时域

2.Filtering = Convolution (= Averaging) - 卷积
转换成频域频率信号,原始信号的任何一个位置,取周围的数量,做一个加权平均,只要再将平均后的信号,逆傅立叶变换回时域就可以得到模糊后的图像(时域)
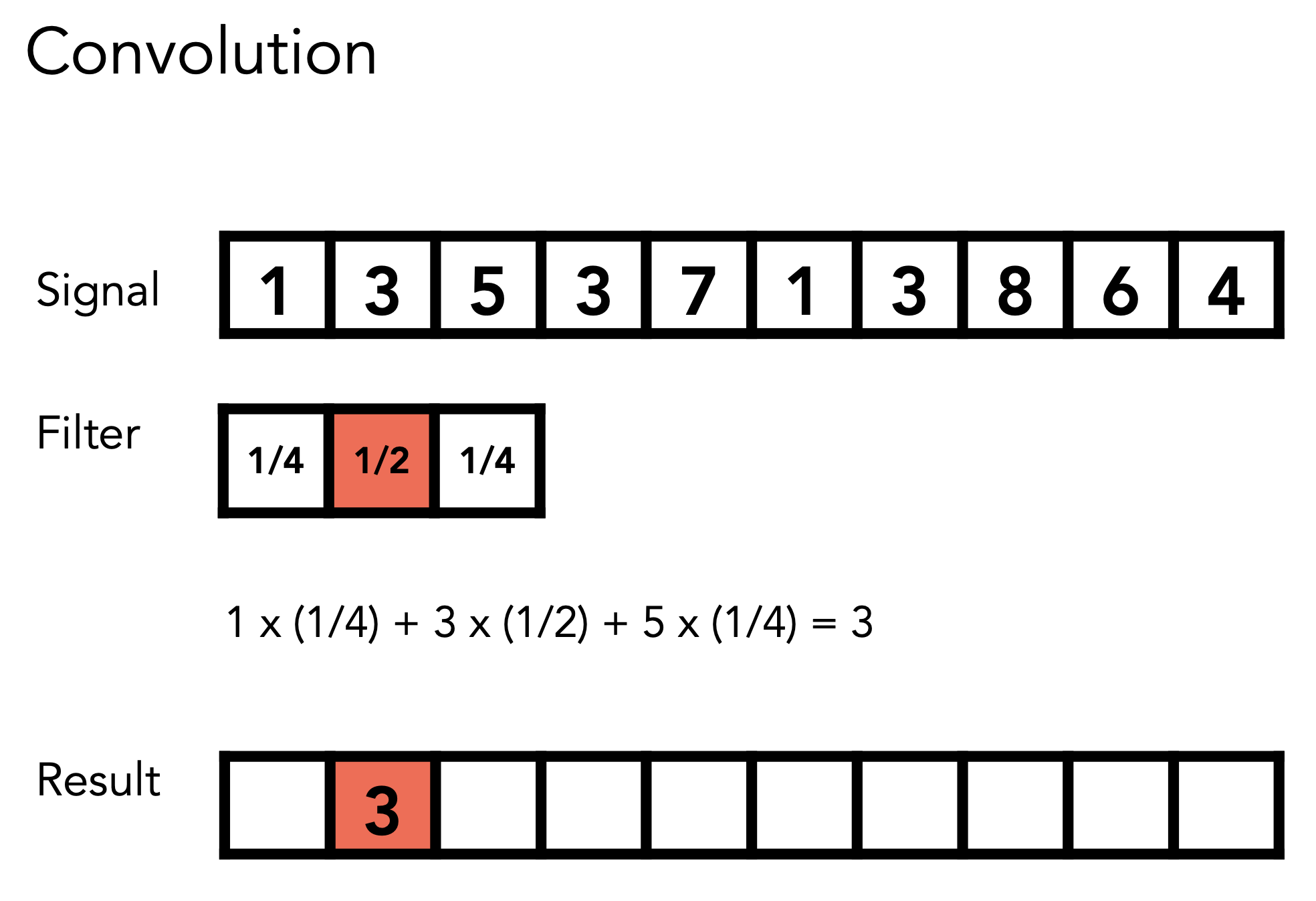

总结:
时域的 ‘卷积’ 等于频域的 ‘乘积’ 在频域中,反之亦然

卷积炒作后需要做一个数量平均,否则会过亮
1 x 1 + 1 x 1 + 1 x 1 +…+ 1 x 1 = 9
9 * * 1/9 = 1

在屏幕空间中,一个像素显示一个三角形时可能存在多种情况,覆盖50%,覆盖30%,覆盖100%,覆盖率从0-100%不等
对于任何一个像素内部,我们都对覆盖面积求一个平均(卷积),如果覆盖了1/8,就是7/8的亮度,覆盖了1/2,就是1/2的亮度,像素内部的值平均起来,这样就不会明显的亮度边界,出现锯齿,会有一个过渡的效果



MSAA
用更多的采样点进行采样,一个像素内虚拟出更多的小的像素点进行采样,同样会消耗更多的计算量,指数级的增长计算量
1个像素4个虚拟点,就是1920x1080x4




