算法时间空间复杂度

1.Big-Oh video

1.描述函数的渐进行为
2.非正式解释 (for 15112): 忽略所有低阶项和常量级
3.正式解释 (after 15112): 维基百科
4.一些例子:
3n^2 - 2n + 25 is O(n^2)
30000n^2 + 2n - 25 is O(n^2)
0.00000000001n^2 + 123456789n is O(n^2)
10nlog_17^n + 25n - 17 is O(nlogn)

2.常见函数族

图示(借用图片来自这里)

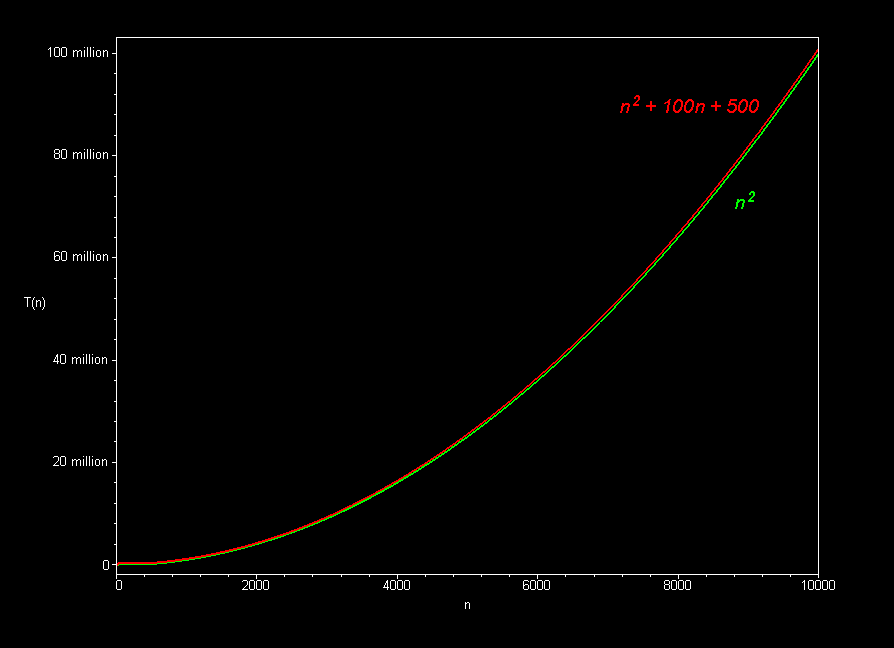
3.效率

当我们说程序程序运行在O(f(N)),我们的意思是

N是我们输入的大小
例如一个字符串s, 那么N = s的大小
例如一个列表L, 那么N = 列表的大小（也适用于集合，字典，和其他集和）
例如一个整数n, 那么N = numberOfDigits(n)(n的位数,字节) = logb(n)(n的对数，b^N的指数)，所以 n = b^N（当b是基数时，你可以使用任何>= 2的基数b）
在文献中，N通常是写成小n，但是我们使用在这里通常表示整数n，不同是不只指代一个数的大小,我们使用大写N来表示输入的大小
f(N) = 我们程序的资源消耗
资源可以是时间，空间，带宽
在15112这个课程，我们主要关心的是时间
对于时间,我们通常计量的是算法的步数而不是运行时长（这里给的算法性能和复杂度都一样,算法步数会更容易去准确描述和推导，算法的运行步数通常等同于时间呈正相关）
这里有多重意思，可以是你记录的计算的最差情况或正常情况，或其他比如最好情况（哪些通常是微不足道的计算量，在实践中不是很有用的），还有经常意味着的意思是最坏的情况，这比平均情况更为实用，总体上更容易计算。
计算书面算法中的步骤，或列表中的比较和交换等
可以通过以下函数验证代码的执行时间：time.time（）

4.好的建议

每个函数族的效率都要比前一个函数更快(只关心最高复杂度的函数，之后的函数效率要做到比之前复杂度高的更快)

还有，在当今的计算机，任何基础的功能函数通常都能达到最小n的复杂度，所以我们只关心比较大的n的复杂度 (n小的话随便什么算法，n比较大的话就要注意算法的效率了)
所以，常量级的复杂度几乎和基础函数一样不那么重要对于性能的影响 (一个算法中有超过常量级的复杂度函数，那么常量级的复杂度的函数可以忽略掉不考虑它的性能影响)
几乎…
不要过早的优化你的代码
相反：认真思考你的算法 (不要在复杂度最低的地方去优化，考虑复杂度高的地方去优化)